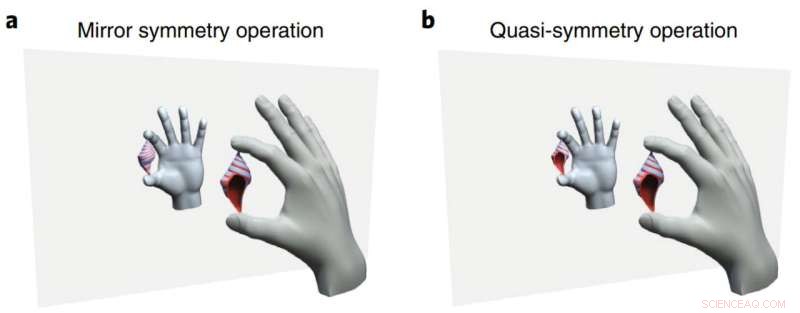
Comparación entre una operación de simetría especular y cuasisimetría. Una operación de simetría especular actúa consistentemente sobre todo el objeto. En contraste, la operación de cuasi-simetría actúa de manera diferente en diferentes partes del sistema. Crédito:MPSD / Departamento de Materia Cuántica Microestructurada
Desde el descubrimiento del efecto Hall cuántico (Premio Nobel 1985), la simetría ha sido el principio rector en la búsqueda de materiales topológicos. Ahora, un equipo internacional de investigadores de Alemania, Suiza y EE. UU. ha introducido un principio rector alternativo, la "cuasisimetría", que conduce al descubrimiento de un nuevo tipo de material topológico con un gran potencial para aplicaciones en espintrónica y tecnologías cuánticas. Este trabajo ha sido publicado en Nature Physics .
A diferencia de una simetría propia que actúa uniformemente sobre todo el objeto, la operación de cuasisimetría actúa selectivamente sobre diferentes partes del sistema. Un ejemplo simplificado puede ser una imagen especular incompleta, en la que algunas partes del objeto se reflejan pero otras no. Teóricamente, corresponde a un sistema que tiene simetría exacta cuando se toma en consideración solo la aproximación básica mientras que los términos aproximativos adicionales rompen dicha simetría. En la estructura de banda electrónica de un sólido, esto impone brechas de energía finitas pero paramétricamente pequeñas en algunos puntos de baja simetría en el espacio de momento.
En su nuevo trabajo, los investigadores demuestran que la cuasisimetría en el semimetal CoSi estabiliza pequeños espacios de energía en un gran plano casi degenerado. Esto se refleja en la forma en que los electrones se doblan en movimiento circular por un campo magnético, conocido como oscilaciones cuánticas. La aplicación de la deformación en el plano rompe la simetría del cristal que separa solo los puntos degenerados correspondientes, pero los puntos protegidos por cuasisimetría permanecen intactos, observables por nuevas órbitas de ruptura magnética. Estos resultados demuestran una de las características más importantes de la cuasi-simetría:su robustez frente a perturbaciones químicas y físicas.
La mayoría de los materiales topológicos descubiertos en los últimos años requieren una ingeniería precisa de su composición química para que sean relevantes para futuras aplicaciones tecnológicas. Por el contrario, las cuasisimetrías eliminan la necesidad de un ajuste tan fino, ya que las características topológicas se pueden encontrar en cualquier potencial químico arbitrario. Además, los materiales topológicos cuasi-simétricos protegidos son robustos frente a cualquier deformación física que rompa la simetría cristalina. Además, los materiales topológicos cuasi protegidos por simetría son resistentes a las deformaciones físicas que rompen la simetría cristalina, un requisito previo clave para su aplicación tecnológica a través de procesos de película delgada.
Estas características demuestran una nueva clase de materiales topológicos con mayor resistencia a las perturbaciones, lo que simplifica su uso en tecnología. Los investigadores creen que este primer ejemplo representa un paso importante para descubrir materiales topológicos más allá de las clasificaciones habituales de grupos espaciales, lo que podría ayudar a la comunidad a no pasar por alto lo que puede estar oculto a simple vista. Observación de superconductividad no trivial en la superficie del semimetal Weyl tipo II