Diagrama de enlace del enlace electrónico cuántico en el espacio de cantidad de movimiento (velocidad) observado en el imán topológico de Weyl Co2 MnGa, determinado a partir de mediciones de espectroscopia de fotoemisión avanzada. Crédito:Ilya Belopolski y M . Zahid Hasan, Universidad de Princeton
A medida que los físicos profundizan en el reino cuántico, descubren un mundo infinitesimalmente pequeño compuesto por una extraña y sorprendente variedad de enlaces, nudos y vueltas. Algunos materiales cuánticos exhiben remolinos magnéticos llamados skyrmions, configuraciones únicas descritas como "huracanes subatómicos". Otros albergan una forma de superconductividad que se tuerce en vórtices.
Ahora, en un artículo publicado en Nature Un equipo de físicos dirigido por Princeton ha descubierto que los electrones en la materia cuántica pueden vincularse entre sí de formas nuevas y extrañas. El trabajo reúne ideas en tres áreas de la ciencia (física de materia condensada, topología y teoría de nudos) de una nueva manera, lo que plantea preguntas inesperadas sobre las propiedades cuánticas de los sistemas electrónicos.
La topología es la rama de las matemáticas teóricas que estudia las propiedades geométricas que pueden deformarse pero no cambiarse intrínsecamente. Los estados cuánticos topológicos llamaron la atención del público por primera vez en 2016 cuando tres científicos, incluido Duncan Haldane, profesor de física matemática Thomas D. Jones de Princeton y profesor de física de la Universidad Sherman Fairchild, recibieron el Premio Nobel por su predicción teórica de la topología en materiales electrónicos.
Desde entonces, los investigadores han buscado expandir esta área de investigación para crear una comprensión más profunda de la mecánica cuántica, como en el campo de la "topología cuántica", que busca explicar el estado de un electrón descrito por una propiedad llamada función de onda. Este fue el catalizador que condujo a la investigación actual, dijo M. Zahid Hasan, profesor de Física Eugene Higgins en la Universidad de Princeton y autor principal del estudio.
"Estamos estudiando propiedades relacionadas con la forma de las funciones de onda de los electrones", dijo Hasan. "Y ahora hemos llevado el campo a una nueva frontera".
El bloque de construcción esencial de esta nueva frontera es una estructura mecánica cuántica conocida como bucle de Weyl, que implica el enrollamiento de funciones de onda de electrones sin masa en un cristal. En un trabajo innovador anterior, publicado en Science en 2019, se descubrieron los bucles de Weyl sin masa en un compuesto compuesto de cobalto, manganeso y galio, con fórmula química Co2 MnGa. Esta investigación fue dirigida por Hasan e incluyó a muchos de los autores del nuevo estudio. En ese momento, entendieron que los bucles de Weyl sin masa producen comportamientos exóticos bajo campos eléctricos y magnéticos aplicados. Estos comportamientos persistieron hasta la temperatura ambiente.
Por sí mismo, un bucle de Weyl es un ejemplo del tipo de devanado de función de onda cuántica que ya es bien conocido. "Los ejemplos anteriores de topología en física a menudo involucraban el devanado de funciones de onda mecánicas cuánticas", dijo Hasan, quien dirigió la investigación actual. "Estos han sido el foco de atención de la comunidad física durante al menos la última década". Estas ideas se derivan de los trabajos anteriores del equipo sobre cristales hechos de rodio y silicio (RhSi), así como materiales llamados imanes de Chern hechos de los elementos terbio, magnesio y estaño (TbMn6 Sn6 ). Ambos descubrimientos fueron dirigidos por el grupo del profesor Hasan y publicados en Nature en 2019 y luego en Nature en 2020.
Sin embargo, el caso de Co2 MnGa resultó ser diferente del devanado de función de onda considerado en las teorías topológicas convencionales. "Aquí, en cambio, tenemos bucles enlazados:nuestra topología anudada recién descubierta es de una naturaleza diferente y da lugar a diferentes números de enlace matemáticos", dijo Tyler Cochran, estudiante graduado en el Departamento de Física de Princeton y coautor del nuevo estudio. /P>
El Co2 Los materiales de MnGa fueron cultivados por la profesora Claudia Felser y su equipo en el Instituto Max Planck de Física Química de Sólidos en Alemania.
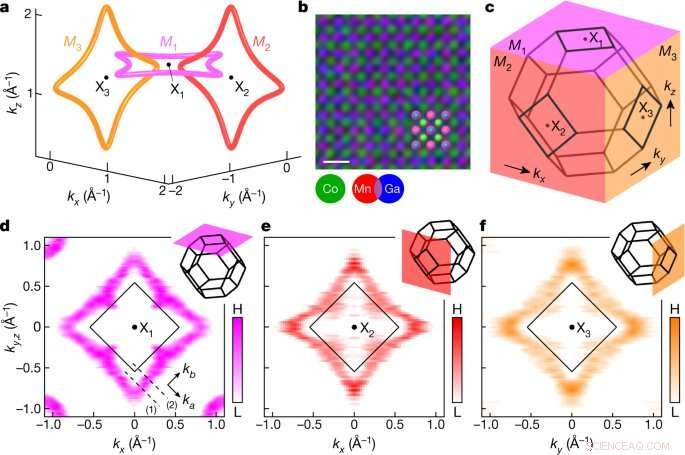
Firmas de bucles de nodos vinculados en Co2 MnGa. Crédito:Naturaleza (2022). DOI:10.1038/s41586-022-04512-8
Una idea esencial surgió cuando el equipo de Princeton calculó y entendió que ciertos materiales cuánticos como el Co2 MnGa podría albergar múltiples bucles de Weyl al mismo tiempo. "Cuando coexisten varios bucles de Weyl, es natural preguntarse si pueden unirse y anudarse de ciertas maneras", dijo Hasan.
Esta realización por parte del equipo de Hasan generó preguntas fundamentales sobre los bucles de Weyl vinculados y reunió a un equipo de expertos de todo el mundo en espectroscopia de fotoemisión, topología matemática, síntesis de material cuántico y cálculos cuánticos de primeros principios para comprender más profundamente la topología de enlace y el anudado en la materia cuántica. .
Para observar el vínculo de forma experimental, el equipo internacional colaboró durante más de cinco años para ampliar sus trabajos anteriores sobre imanes topológicos. El equipo realizó experimentos avanzados de espectroscopia de fotoemisión en instalaciones de radiación de sincrotrón de vanguardia en los Estados Unidos, Suiza, Japón y Suecia.
"Resultó ser un rompecabezas fascinante que nos mantuvo enganchados por un tiempo", dijo Ilya Belopolski, autora principal del estudio, ex estudiante de posgrado en el laboratorio de Hasan en la Universidad de Princeton y ahora investigadora postdoctoral en el Centro RIKEN de Materia Emergente. Ciencia cerca de Tokio, Japón. "Desentrañar las complejidades de esta elaborada estructura cuántica vinculada requirió más de tres años de mediciones de alta precisión y ultra alta resolución en las principales instalaciones espectroscópicas del mundo".
El análisis de los datos experimentales reveló un objeto contrario a la intuición plegado sobre sí mismo y envuelto en un toro de dimensiones superiores. "Comprender la estructura del objeto requería un nuevo puente entre la mecánica cuántica, la topología matemática y la teoría de nudos", dijo Guoqing Chang, autor del estudio que ahora es profesor asistente de física en la Universidad Tecnológica de Nanyang en Singapur. Mientras era un ex investigador postdoctoral que trabajaba con Hasan en Princeton, Chang dirigió uno de los primeros estudios teóricos de la topología de enlaces en 2017 en un trabajo pionero en Physical Review Letters .
De hecho, el equipo de investigación descubrió que la teoría cuántica de materiales existente no podía explicar adecuadamente la aparición de esta estructura. Pero la teoría de los nudos, reconocieron, podría contener algunas pistas.
"Nos dimos cuenta de que algunos aspectos de la teoría de nudos son muy poderosos para explicar las propiedades cuánticas de los materiales topológicos que no se entendían antes", dijo Hasan. "Este es el primer ejemplo que conocemos donde se ha aplicado la teoría de nudos para comprender el comportamiento de los imanes topológicos. Y esto es muy emocionante".
Los hallazgos continúan y amplían la conversación de décadas entre la física y la topología, esta vez aportando nuevas ideas matemáticas para explicar los experimentos sobre ferromagnetos cuánticos. "Históricamente, algunos de los descubrimientos científicos más importantes surgieron cuando los humanos notaron nuevas conexiones entre las matemáticas y los fenómenos naturales. Siempre es emocionante encontrar ejemplos inesperados de matemáticas sutiles en nuestros experimentos", dijo Hasan. "Aún más, fue interesante que la conexión matemática estuviera en el campo de la topología, que ha seguido surgiendo una y otra vez en diferentes formas en el estudio de los materiales cuánticos".
Los investigadores tienen la intención de expandir su investigación en múltiples direcciones. Aunque Hasan y su equipo centraron sus esfuerzos en el comportamiento de los imanes topológicos, sostienen que la teoría tiene el potencial de ayudar a explicar otros comportamientos cuánticos. "Creemos que la teoría de nudos también se puede aplicar a muchos otros conductores topológicos, superconductores, qubits y muchas otras cosas", dijo.
Y aunque los investigadores no estaban pensando en aplicaciones prácticas, "estuvimos involucrados en la investigación fundamental", enfatizó Hasan, sus conocimientos podrían ayudar en el desarrollo de la computación cuántica, especialmente en el desarrollo de nuevos tipos de qubits topológicos. Avances y perspectivas en materiales topológicos magnéticos