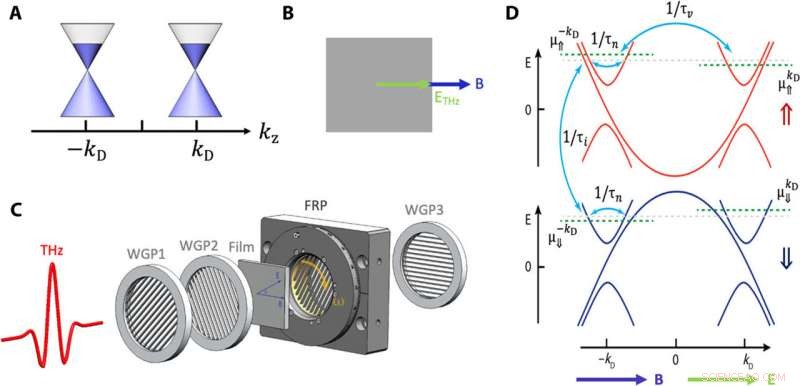
Dinámica de carga de la anomalía quiral en un DSM y la configuración experimental. (A) Ilustración esquemática de la estructura electrónica de baja energía del DSM Cd3As2. Alberga dos nodos de Dirac 3D ubicados a lo largo del eje kz. (B) Se espera la anomalía quiral cuando el campo magnético de cd y el campo eléctrico THz están alineados. (C) Esquema del espectrómetro de magnetoterahercios en el dominio del tiempo utilizado para recopilar datos. El polarizador de rejilla de alambre 1 (WGP1) y WGP2 se utilizan para producir pulsos de terahercios polarizados linealmente con ETHz ∥ B o ETHz ⊥ B. Se utiliza un polarizador de rotación rápida (FRP) para modular el campo eléctrico de terahercios en una frecuencia cercana a 47 Hz. Con WGP3 y amplificador de bloqueo, la compleja matriz de transmisión se puede determinar mediante una única medición con alta precisión. (D) En un DSM con ETHz ∥ B, los estados 3D de Dirac desarrollarán niveles de Landau (LL), que se dispersan a lo largo de la dirección del campo magnético. El cero LL da la corriente quiral. Varias tasas de relajación diferentes controlan la dinámica de carga. 1 / τn es la tasa de dispersión intranodo (normal), 1 / τv es la tasa de dispersión por intervalos, y 1 / τi es la tasa de dispersión de entrenudos en el mismo valle de momento, pero a la otra variedad isospin. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
Los semimetales 3D Dirac y Weyl se pueden caracterizar por una quiralidad de carga con el bloqueo paralelo o antiparalelo del espín del electrón en su momento. Dichos materiales pueden exhibir un efecto magnético quiral asociado con la conservación cercana de la carga quiral. En este trabajo, Bing Cheng y un equipo de investigación en física y astronomía en la Universidad Johns Hopkins y ciencia de materiales en la Universidad de California, Santa Bárbara, utilizó espectroscopía magneto-terahercios para estudiar el arseniuro de cadmio epitaxial (Cd 3 Como 2 ) películas:un material ampliamente explorado en la física del estado sólido para extraer sus conductividades en función del efecto magnético quiral. Cuando el equipo aplicó el campo, notaron una respuesta de Drude marcadamente aguda, un modelo muy aclamado de transporte electrónico sugerido por el físico Paul Drude hace más de 100 años. La respuesta de Drude surgió del contexto más amplio de este sistema como una firma definitiva de un nuevo canal de transporte consistente con la respuesta quiral. La independencia de campo de la relajación quiral estableció que fue establecida por la conservación aproximada de la isospina en la configuración.
La anomalía quiral
Algunas de las demostraciones más notables de los estados topológicos de la materia surgen de su respuesta a los campos electromagnéticos. Por ejemplo, Los aisladores topológicos se caracterizan por un efecto magnetoeléctrico cuantificado. El semimetal de Weyl y los semimetales de Dirac (WSM y DSM) son estados de la materia en los que las bandas de conducción y valencia se tocan y se dispersan casi linealmente alrededor de pares de nodos en el espacio de momento. Cada nodo puede identificarse por su quiralidad relativa al giro de una partícula sin masa (dispersión lineal) orientada paralela o antiparalela a su momento. Por tanto, los sistemas de Dirac son similares a dos copias de los sistemas de Weyl; en cada nodo, hay dos conjuntos de bandas de dispensación lineales con carga quiral opuesta. A pesar de ser metales, Los semimetales de Weyl y los semimetales de Dirac mostraron distintos efectos de transporte asociados con la conservación cercana de la carga quiral. Por lo tanto, la anomalía quiral existía en los límites de transporte cuántico y semiclásico. La carga quiral no se conserva en ningún material real debido a violaciones de la simetría quiral a través de dispersiones de bandas no lineales. Como resultado, la casi conservación de la carga quiral es relativa a la simetría quiral emergente de baja energía. Si bien el efecto existió en regímenes de transporte semiclásico y cuántico, el efecto se comprendió mejor en el límite cuántico. La carga quiral no se conserva con precisión y se bombea bajo la acción de campos eléctricos y magnéticos colineales denominados anomalía quiral. Los científicos han observado una magnetorresistencia longitudinal negativa (NLMR) en varios sistemas semimetálicos de Dirac y semimetálicos de Weyl como consecuencia del efecto magnético quiral, aunque NLMR no es causado exclusivamente por este efecto.
Conductividad de terahercios en diferentes campos magnéticos. (A) ETHz ∥ B con B∥ (1¯10) para la muestra S1. La anomalía quiral hace que la conductividad de terahercios σ1 por debajo de 1 THz sea mejorada gradualmente por el campo magnético. (B) ETHz ⊥ B con B∥ (1¯10) para la muestra S1. La supresión de la conductividad de terahercios σ1 es la firma de la magnetorresistividad positiva, que se observa generalmente en campos eléctricos y magnéticos perpendiculares. (C) ETHz ∥ B para B∥ (11¯¯¯¯2) muestra S2. (D) ETHz ⊥ B para B∥ (11¯¯¯¯2) muestra S2. (E y F) Comparaciones de estos datos de 0 y 7 T y sus diferencias para las muestras S1 y S2. Δσ1 es la conductividad quiral intrínseca de la anomalía quiral. El área gris resaltada representa la fuerza del efecto de bombeo de carga, y su ancho define la tasa de relajación quiral. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914 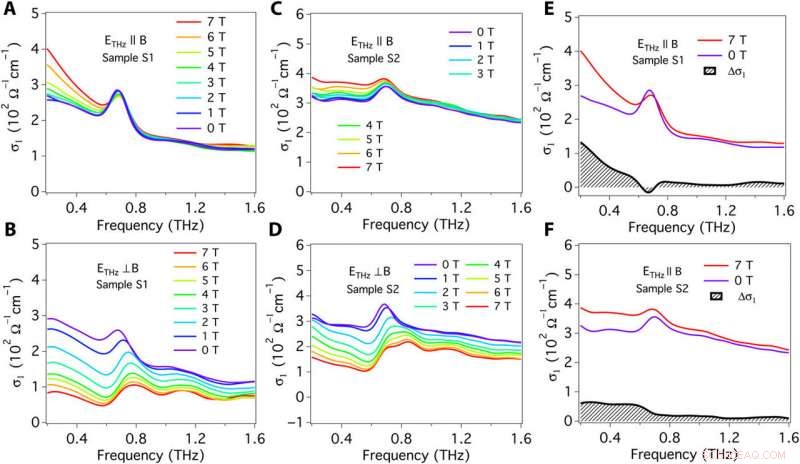
Un parámetro clave que gobierna la anomalía quiral es la tasa de relajación quiral. Las propiedades intrínsecas de la anomalía quiral pueden caracterizarse de manera más convincente midiendo directamente la tasa de relajación quiral y las tasas de relajación intravalle. King y col. utilizó espectroscopía de magneto-terahercios para estudiar las películas delgadas epitaxiales de alta calidad de semimetales de Dirac arseniuro de cadmio (Cd 3 Como 2 ). Este es un material ideal para investigaciones debido a sus nodos de Dirac cuádruples degenerados que están protegidos por una C 4 simetría. Típicamente, el Cd orientado de alta calidad 3 Como 2 las películas se pueden cultivar usando epitaxia de haz molecular. Al realizar experimentos de conductividad dependiente de la frecuencia, los científicos extrajeron directamente tanto la tasa de relajación quiral como la tasa de relajación intravalle. Luego midieron dos Cd 3 Como 2 películas y extrajeron su conductividad de terahercios dependiente del campo utilizando dos mediciones sin contacto para evitar cualquier artefacto asociado con las rutas de corriente no homogéneas que tienden a plagar los experimentos de corriente continua.
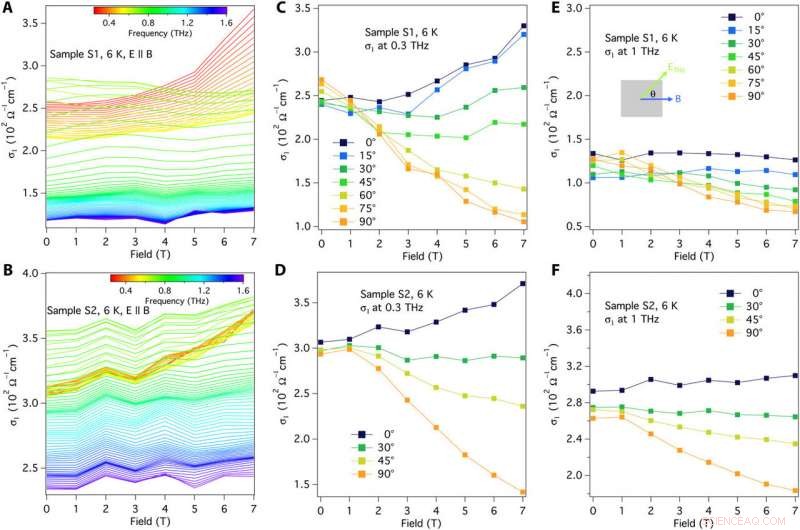
Conductividad de terahercios en diferentes campos magnéticos. Conductividad en terahercios σ1 en cada frecuencia (ver escala de barras de color) en función del campo magnético de (A) muestra S1 y (B) muestra S2 con ETHz ∥ B. Conductividad en terahercios (a 0.3 THz) como función del campo magnético bajo diferentes ángulos de polarización de terahercios de (C) muestra S1 y (D) muestra S2. La configuración del ángulo de polarización θ entre el campo eléctrico de terahercios y el campo magnético se muestra en el esquema de (E). Conductividad de terahercios (a 1 THz) como función del campo magnético bajo diferentes ángulos de polarización de terahercios de (E) muestra S1 y (F) muestra S2. Todos los datos se tomaron en 6 K. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
Conductividad de terahercios y transporte quiral
A continuación, el equipo investigó la conductividad de terahercios en diferentes campos magnéticos y extrajo el bombeo de carga dinámica y la relajación de la anomalía quiral utilizando ajustes de Drude-Lorentz. Notaron un notable efecto inducido por el campo que resultó en una mejora de solo la conductividad de baja frecuencia. Sin embargo, esto no fue el resultado de un cambio en la tasa de dispersión normal o un cambio en la densidad de portadora del material, sino que se basó en la aparición de un canal de transporte paralelo con una nueva escala de frecuencia. El efecto tampoco se asoció con la dispersión dependiente de espín, que normalmente se manifestaría como un cambio general en la tasa de dispersión. La aparición de un canal de transporte adicional y una nueva escala de tiempo coincidió precisamente con las expectativas teóricas de la anomalía quiral. El transporte quiral se produjo mediante la acumulación del potencial electroquímico efectivo a través del equilibrio entre el bombeo quiral y la dispersión de entrenudos. Para distinguir una corriente quiral de estado estable, la tasa de dispersión quiral tenía que ser menor que la tasa de relajación intravalle. En los experimentos, Cheng y col. señaló que la tasa de dispersión quiral es aproximadamente un cuarto de la tasa de relajación intravalle en ambas muestras. Los científicos compararon este tamaño relativo a la luz de la teoría predominante y esperan realizar más estudios en esta área en el futuro. El equipo también interpretó los recientes experimentos de terahercios no lineales relativos a la relajación quiral que mostraron una velocidad lenta debido a una mayor separación de nodos en el arseniuro de tantalio cristalino semimetal de Weyl (taAs) y / o la falta de dispersión de isospin.
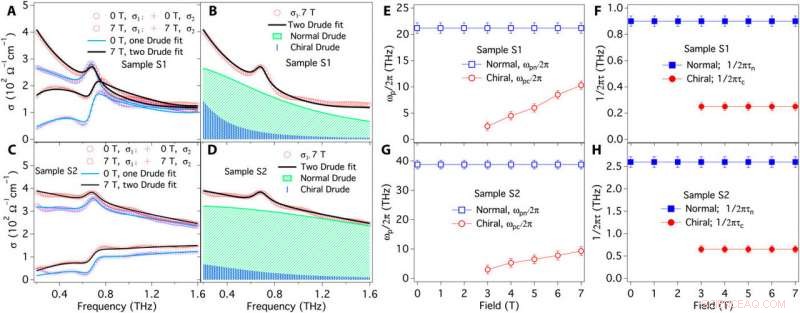
Bombeo de carga dinámica y relajación de la anomalía quiral extraída por ajustes de Drude-Lorentz. (A y B) Se ajusta a la conductividad de terahercios de la muestra S1 con ETHz ∥ B. El oscilador Drude más nítido (área sombreada en azul) representa el nuevo canal de transporte de la anomalía quiral. (C y D) Se ajusta a la conductividad de terahercios de la muestra S2 con ETHz ∥ B. Frecuencia de plasma Drude dependiente del campo en la muestra S1 (E) y la muestra S2 (G). Las frecuencias plasmáticas del canal de transporte quiral (ωpc / 2π, rojo) corresponden directamente al bombeo de cargas quirales y son funciones lineales de campo. Tasas de dispersión en la muestra S1 (F) y la muestra S2 (H). Las tasas de dispersión quiral (1 / 2πτc, rojo) controlan el proceso dinámico de anomalía quiral como se muestra en la Fig.1D, y en ambas muestras, son mucho más pequeñas que las tasas de dispersión masiva normales (1 / 2πτn, azul). Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
panorama
De este modo, Bing Cheng y sus colegas observaron un efecto anómalo de magnetoconductividad de terahercios en el arseniuro de cadmio semimetálico de Dirac. El efecto dependía del efecto magnético quiral. La dependencia y evolución observadas de la forma funcional de la conductividad estaba en concordancia precisa con la teoría de la anomalía quiral. Sin embargo, las tasas de dispersión quiral e intranodo no coincidían precisamente con la teoría predominante, ya que la dispersión quiral fue mucho más fuerte de lo previsto. Por lo tanto, los investigadores desarrollarán modelos más revisados con tasas más realistas de dispersión de impurezas experimentales en el futuro.
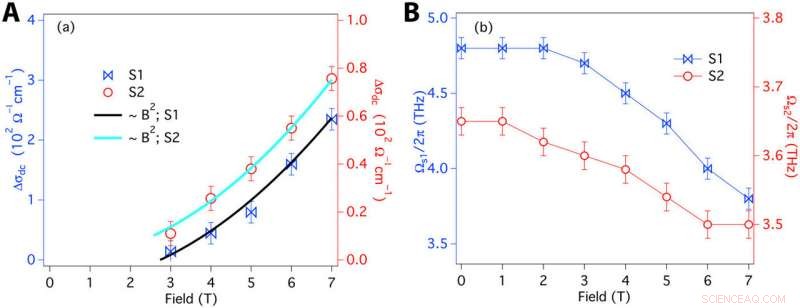
Conductividad quiral de cc intrínseca extrapolada de la conductividad en terahercios. (A) Magnetoconductividad de cc intrínseca de anomalía quiral en la muestra S1 (azul) y la muestra S2 (rojo). En ambas muestras, Δσ sigue a B2, coherente con la predicción de la dependencia de campo de la corriente quiral en el régimen de transporte semiclásico. (B) Fuerza del oscilador de fonón en la muestra S1 (azul) y la muestra S2 (rojo). Las intensidades del oscilador en ambas muestras disminuyen a medida que el campo magnético mejora la conductividad quiral. Crédito:Science Advances, doi:10.1126 / sciadv.abg0914
© 2021 Science X Network