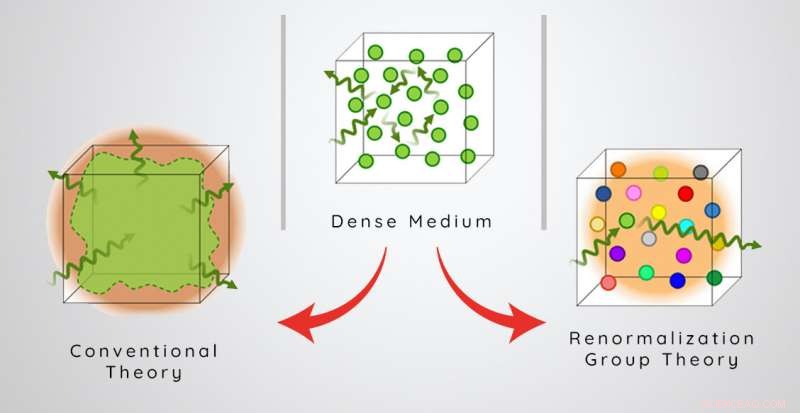
Ilustración esquemática de la respuesta óptica de un medio atómico denso visto por las teorías tradicionales frente a la teoría RG. Crédito:ICFO
Portada de Pink Floyd's Dark Side of the Moon, votado como el mejor álbum de rock clásico de todos los tiempos, pretendía retratar el prisma y la dispersión de la luz en un arco iris como un cierto simbolismo metafórico y un espectáculo de luces que nunca se celebró. Sin embargo, realmente no sabían que muchos usarían esta imagen para ayudar a ilustrar el concepto de índice de refracción y cómo la luz cambia de velocidad y dirección cuando se encuentra con un medio diferente.
Aunque conceptualmente el dibujo no era exacto, transmitió el mensaje de que la luz cambia su velocidad cuando se mueve a otro medio, y que las diferentes velocidades de los diferentes colores hacen que la luz blanca se disperse en sus diferentes componentes. Este cambio de velocidad está relacionado con el índice de refracción, un número sin unidad que representa la relación entre la velocidad de la luz en el vacío y la velocidad de la luz en un medio.
En general, todos los materiales con índices de refracción positivos tienen valores cercanos a 1 para la luz visible. Nunca se ha explicado si esto es solo una coincidencia o refleja algo de física más profunda.
Ahora, en un estudio reciente publicado en Revisión física X y destacado por los editores, Los investigadores del ICFO Francesco Andreoli y el profesor ICREA en ICFO Darrick Chang, en colaboración con investigadores de la Universidad de Princeton, Universidad de Chicago e Institut d'Optique, han investigado y explicado por qué el índice de refracción de un gas atómico diluido solo puede alcanzar un valor máximo de 1,7, independientemente de cuán alta sea la densidad de átomos.
Este resultado contrasta con las teorías convencionales de los libros de texto, que predicen que cuanto más material hay, cuanto mayor pueda ser la respuesta óptica y el índice de refracción. El desafío de comprender correctamente el problema tiene que ver con la dispersión múltiple de la luz (todos los caminos complejos que la luz puede atravesar dentro de un medio) y la interferencia resultante. Esto puede hacer que cada átomo individual vea una intensidad de luz local que es muy diferente a la intensidad enviada, y que varía en función de la geometría de los átomos que lo rodean. En lugar de ocuparse de los complejos detalles microscópicos de esta granularidad, Los libros de texto a menudo asumen de alguna manera que esta granularidad y sus efectos sobre la luz pueden suavizarse.
A diferencia de, los equipos hacen uso de una teoría, llamado grupo de renormalización de trastorno fuerte (RG), lo que les permite capturar granularidad y múltiples efectos de dispersión de una manera sencilla. Esta teoría muestra que la respuesta óptica de cualquier átomo dado se ve afectada de manera desproporcionada por su vecino más cercano debido a las interacciones de campo cercano, razón por la cual fallan las teorías típicas de suavizado. El efecto físico de las interacciones de campo cercano es producir un ensanchamiento no homogéneo de las frecuencias de resonancia atómica, donde la cantidad de ensanchamiento crece con la densidad. Por lo tanto, no importa cuán alta sea la densidad física de los átomos, la luz entrante de cualquier frecuencia solo verá alrededor de 1 átomo casi resonante por longitud de onda cúbica para dispersarse de manera eficiente, que limita el índice de refracción a su valor máximo de 1,7.
Mas ampliamente, Este estudio sugiere que la teoría RG podría constituir una nueva herramienta versátil para comprender el desafiante problema de la dispersión múltiple de la luz en medios desordenados casi resonantes. incluso en los regímenes no lineal y cuántico. También muestra la promesa de tratar de comprender los límites del índice de refracción de materiales reales, comenzando de abajo hacia arriba a partir de los átomos individuales que los componen.