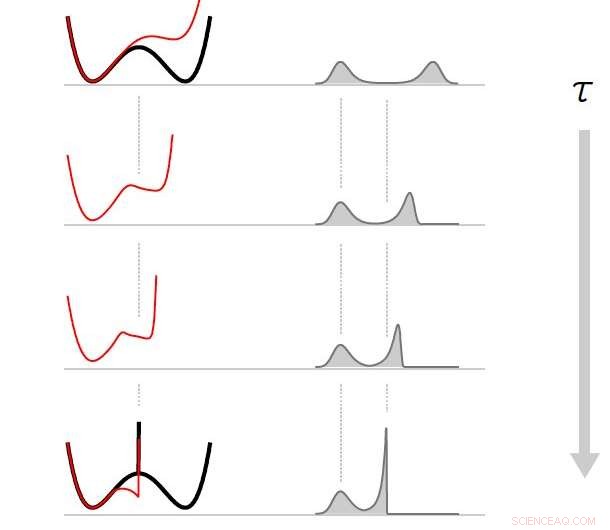
Crédito:Proesmans, Ehrich y Bechhoefer
La teoría de la termodinámica estocástica es un marco que delinea la cantidad de calor, dinámica y entropía en pequeño (es decir, mesoscópicos) sistemas que están lejos de un estado de equilibrio termodinámico. En años recientes, Los científicos han intentado utilizar esta teoría para comprender mejor la dinámica subyacente a una variedad de sistemas, incluyendo partículas coloidales, ADN ARN, enzimas motores moleculares y dispositivos electrónicos.
En un artículo publicado recientemente en Cartas de revisión física , Los investigadores de la Universidad Simon Fraser combinaron la termodinámica estocástica con otra construcción conocida como teoría del transporte óptimo, con el objetivo de revelar el costo termodinámico asociado con el borrado de un solo bit de información de un dispositivo durante un período de tiempo definido. La teoría del transporte óptimo es un marco introducido a finales del siglo XVIII que responde a preguntas como:"Si uno tiene que mover tierra de la pila A a la pila B, ¿Cómo se debe transportar para minimizar el esfuerzo requerido para transportarlo de un lugar a otro? "
Hace aproximadamente una década, El físico teórico Erik Aurell y otros investigadores se dieron cuenta de que la teoría del transporte óptimo también podría usarse para resolver una variedad de problemas de optimización enraizados en el campo de la termodinámica. En su estudio reciente, el equipo de investigadores de la Universidad Simon Fraser realizó cálculos basados en una técnica presentada por Aurell y sus colegas.
"Nuestro artículo se basa en el marco general de la termodinámica estocástica, "Karel Proesmans, uno de los investigadores que realizó el estudio, dijo Phys.org. "Al combinar esta teoría con ideas de la teoría del transporte óptimo, es posible calcular el costo termodinámico mínimo de un proceso en desequilibrio. Usamos estas ideas para generalizar el principio de Landauer a procesos de tiempo finito ".
Principio de Landauer, el principio principal que describe la termodinámica del procesamiento de la información, establece un límite teórico inferior para la energía consumida por un dispositivo al realizar un cálculo determinado. Por lo tanto, también proporciona un valor específico que representa el costo termodinámico mínimo de borrar información de un dispositivo (es decir, kT ln2 por bit, donde k es la constante de Boltzmann y T es la temperatura del ambiente circundante).
Este costo mínimo, sin embargo, Por lo general, solo se logra para operaciones que se realizan muy lentamente. En su estudio, por otra parte, Proesmans y sus colegas se propusieron identificar la forma más eficiente posible de borrar un poco de un dispositivo rápidamente dentro de un período de tiempo establecido.
"Hemos derivado protocolos que minimizan el trabajo necesario para borrar un poco de información en un período de tiempo determinado, asumiendo que tenemos un control completo sobre las fuerzas aplicadas que afectan a la partícula, "Proesmans dijo." Al hacerlo, también obtuvimos un límite inferior simple sobre la cantidad de trabajo necesario para borrar un poco ".
El reciente estudio realizado por Proesmans y sus colegas arrojó dos hallazgos importantes. Primero, los investigadores pudieron calcular los límites superior e inferior de la cantidad mínima de trabajo necesaria para borrar un poco de un dispositivo. En el futuro, estos límites podrían servir como referencia para evaluar el desempeño de dispositivos y plataformas experimentales de última generación. Es más, el marco propuesto por los investigadores podría usarse para construir protocolos óptimos para borrar bits de dispositivos electrónicos.
"Hasta aquí, nos hemos centrado en cálculos teóricos, ", Dijo Proesmans." Nuestro próximo paso será probar nuestro límite en sistemas experimentales. En particular, veremos configuraciones que consisten en partículas coloidales en pinzas ópticas. Otra pregunta interesante que nos gustaría responder es qué tan bien cambia nuestro límite cuando uno tiene un control limitado sobre el sistema ".
© 2020 Science X Network