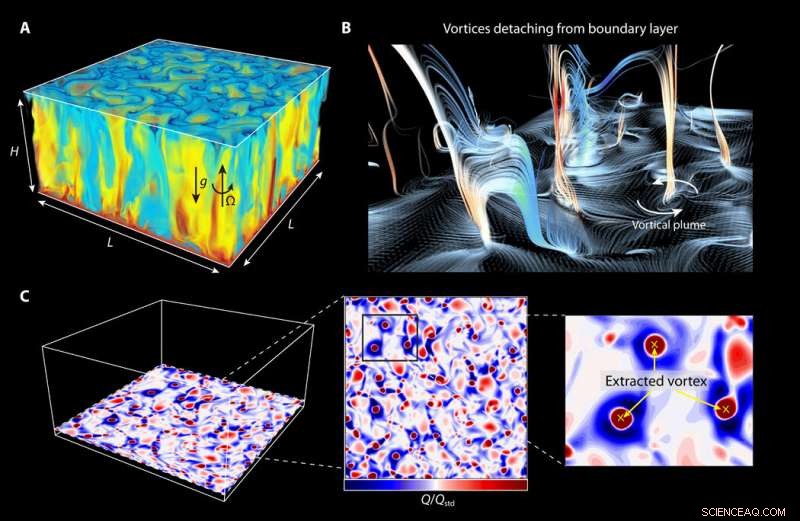
Estructuras de flujo con rotación. Instantáneas de (A) la temperatura θ y (B) líneas de corriente que se originan en la capa límite térmica inferior. (C) Instantáneas de Q / Qstd (criterio Q) tomadas horizontalmente en el borde de la capa límite térmica para el número de Ekman (Ek) =4 × 10−5 y Ra =108 y una demostración del vórtice extraído. Las ubicaciones del centro del vórtice están marcadas como cruces amarillas. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110
El movimiento browniano de partículas en un fluido es un comportamiento colectivo común en los sistemas biológicos y físicos. En un nuevo informe sobre Avances de la ciencia , Kai Leong Chong, y un equipo de investigadores en física, Ingenieria, e ingeniería aeroespacial en China, llevaron a cabo experimentos y simulaciones numéricas para mostrar cómo el movimiento de los vórtices se asemejaba a las partículas brownianas inerciales. Durante los experimentos, el flujo vortical convectivo turbulento giratorio permitió que las partículas se movieran balísticamente al principio y de manera difusa después de un tiempo crítico en una transición conductual directa, sin pasar por un régimen de memoria hidrodinámica. El trabajo implica que los vórtices convectivos tienen memoria inducida por inercia, por lo que su movimiento a corto plazo estaba bien definido en el marco del movimiento browniano aquí por primera vez.
movimiento browniano
Albert Einstein proporcionó por primera vez una explicación teórica del movimiento browniano en 1905 con el movimiento de partículas de polen en un baño termal, el fenómeno es ahora un ejemplo común de procesos estocásticos que ocurren ampliamente en la naturaleza. Más tarde, en 1908, Paul Langevin notó la inercia de las partículas y predijo que su movimiento sería balístico en un corto período de tiempo. cambiando a movimiento difuso después de una línea de tiempo específica. Sin embargo, debido a la rapidez de esta transición, Los investigadores tardaron más de un siglo en poder observar directamente el fenómeno. Sin embargo, el movimiento browniano "puro" predicho por Langevin no se observó en sistemas líquidos y la transición abarcó una amplia gama de escalas de tiempo. La transición lenta y suave se produjo debido al efecto de memoria hidrodinámica, para generar, en última instancia, correlaciones de largo alcance. Los científicos habían observado previamente el efecto de memoria hidrodinámica en múltiples sistemas, incluidas las suspensiones coloidales, partículas suspendidas en el aire y partículas atrapadas en pinzas ópticas. En este trabajo, Chong y col. mostró cómo los vórtices en flujos altamente conectivos se comportaban como partículas inerciales para realizar un movimiento browniano puro, por primera vez, sin ser influenciado por el efecto hidrodinámico. Identificaron y extrajeron los vórtices utilizando el criterio Q (un método para la identificación de vórtices). El trabajo les ayudará a predecir el movimiento del vórtice durante un período de tiempo específico en sistemas astrofísicos y geofísicos.
Movimiento balístico a difusivo de vórtices convectivos. (A) El MSD de los vórtices en función del tiempo. (B) MSD normalizado en función de t / tc. La línea continua representa un ajuste de la ecuación. 4 a los datos. Tanto en (A) como en (B), los símbolos sólidos denotan resultados numéricos en Ra =1 × 108, y los símbolos abiertos denotan resultados experimentales en Ra =3 × 107. (C) Coeficiente de difusión D de vórtices (símbolos abiertos) y la escala de tiempo característica tc para la transición de movimiento (símbolos sólidos) como una función Ra / Rac. (D) Función de autocorrelación de velocidad (VACF) versus t / tc para diferentes Ek. La línea discontinua representa C (t) =2Dtcexp (−t / tc). La línea continua indica una disminución de la ley de potencia para el VACF (los datos para t ≳ 5tc tienen cierta dispersión debido a estadísticas insuficientes). Tenga en cuenta que todas las cantidades físicas se hacen adimensionales como se describe en el texto principal. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110 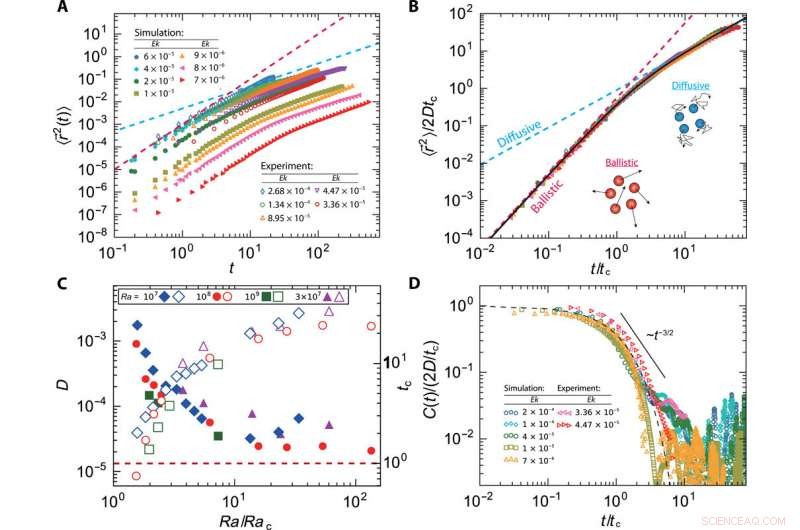
Un desafío existente en la investigación astrofísica y geofísica es predecir el movimiento de los vórtices dentro de un período de tiempo específico. Chong y col. utilizó un sistema modelo para estudiar vórtices en flujos convectivos conocido como convección de Rayleigh Benard (RB), que incluye una capa fluida de altura fija, calentado desde abajo y enfriado desde arriba, mientras se gira sobre el eje vertical a una velocidad angular. La diferencia de temperatura en el sistema desestabilizó el flujo para que ocurriera la convección cuando el impulso térmico era lo suficientemente fuerte. Los científicos utilizaron tres parámetros adimensionales para caracterizar la dinámica del flujo, incluido el número de Rayleigh (Ra), Número de Prandtl (Pr) y el número de Ekman (Ek). En presencia de rotación, Las estructuras en forma de vórtice emergieron como paquetes fluidos que subían o bajaban en espiral. Los investigadores continúan investigando estos penachos vorticales debido a su importancia en el impulso y el transporte de calor.
Chong y col. Primero estudió el movimiento de los vórtices rastreando su cambio de posición a través de una serie de instantáneas. Caracterizaron el comportamiento estadístico de los vórtices utilizando su desplazamiento cuadrático medio (MSD). Los valores de MSD para diferentes Ek y Ra exhibieron un comportamiento similar, lo que indica que en un marco de tiempo corto el movimiento de vórtice se transfirió del movimiento balístico al movimiento difusivo. Esta transición se asemeja al movimiento browniano en un baño termal. Por lo tanto, los científicos trataron los vórtices como partículas brownianas y describieron su movimiento resolviendo la ecuación de Langevin para obtener su MSD. Los resultados implicaron una dinámica similar de movimiento de vórtice para Ra y Ek, lo que sugiere que los vórtices exhibieron un comportamiento "browniano puro". En el sistema de convección, los vórtices transportaban paquetes de fluidos que estaban más calientes y más fríos que el fluido circundante; esta diferencia de densidad relativamente pequeña causada por variaciones de temperatura en el experimento dio lugar al notable comportamiento balístico.
Vórtices que forman un patrón enrejado con una velocidad de rotación suficientemente alta. (A) Instantáneas de Q / Qstd tomadas horizontalmente en el borde de la capa límite térmica para, de izquierda a derecha, Ek =4 × 10−5, 1 × 10−5, y 7 × 10−6 en Ra =108. (B) Función de distribución radial g (r) en función de r / a, donde a es el radio promedio de vórtices. (C) El valor máximo gmax de la función de distribución radial versus Ra / Rac (el caso de Ra =3 × 107 es del experimento, los demás son de DNS). Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110 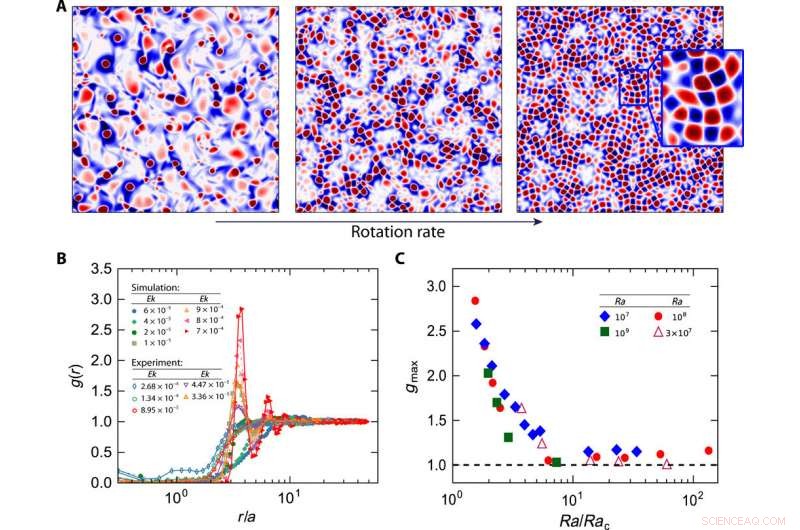
A pesar del movimiento de tipo browniano, la distribución espacial de los vórtices no fue aleatoria, y exhibió estructuras estampadas, que los científicos obtuvieron usando instantáneas de varias tasas de rotación. A medida que variaba el número de Ekman (Ek), Se produjeron varios cambios en la distribución de los vórtices. En primer lugar, el número de vórtices aumentó con la velocidad de rotación, de modo que los vórtices inicialmente diluidos y distribuidos aleatoriamente se volvieron altamente concentrados y agrupados. El aumento de la densidad del número de vórtices con la tasa de rotación también coincidió con investigaciones anteriores. Próximo, cuando la tasa de rotación se vuelve lo suficientemente alta, formaron una estructura de rejilla de vórtice. Cuando Chong et al. ampliado en una región local para observar la tasa de rotación más alta, observaron un patrón regular para tales estructuras de rejilla de vórtices. Las regiones rojizas de los vórtices formaron una red cuadrada y las regiones localizadas azuladas intermedias mostraron un alto comportamiento de deformación. El equipo atribuyó los patrones cuadrados observados en el trabajo a diferentes configuraciones de límites y parámetros de control.
A pesar del movimiento aleatorio en el dominio temporal, los vórtices mostraron un orden espacial específico, lo que resultó en una aparente contradicción. Chong y col. observaron las trayectorias de los vórtices durante la rotación lenta y rápida. Sin embargo, los vórtices no viajaron lo suficientemente lejos para "ver" o interactuar con otros vórtices. Atribuyeron el orden espacial de los vórtices a la competencia entre los dos procesos dinámicos caracterizados por la escala de tiempo de relajación del vórtice y la escala de tiempo browniana. respectivamente.
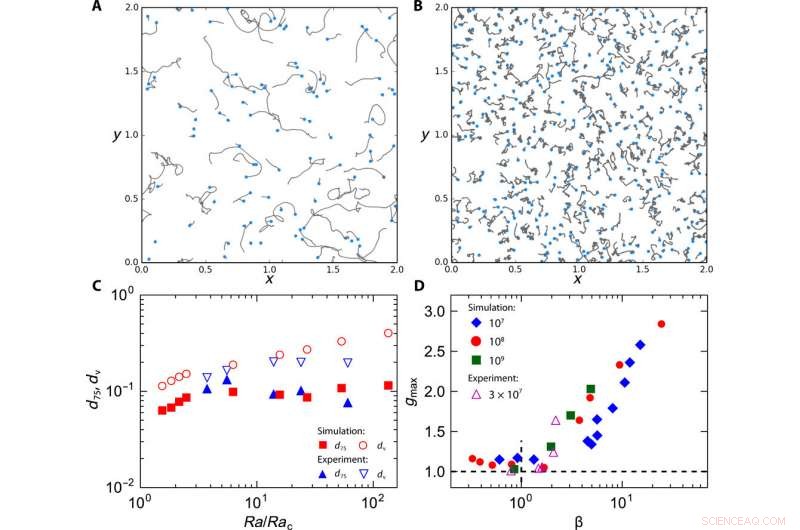
Movimiento localizado de vórtices. Trayectorias de vórtices:(A) Ek =1 × 10−4 y (B) Ek =7 × 10−6; en ambos casos, Ra =1 × 108. Los puntos azules indican el final de las trayectorias. (C) La separación promedio (dv) entre vórtices (símbolos abiertos) y el percentil 75 de la distancia (d75) recorrida por vórtices (símbolos sólidos), en función de Ra / Rac para Ra =1 × 108 (simulación, símbolos rojos) y Ra =3 × 107 (experimento, símbolos azules). (D) La función de distribución radial máxima gmax versus β definida como la relación entre la escala de tiempo browniano y la escala de tiempo de relajación. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110
De este modo, Kai Leong Chong y sus colegas mostraron cómo el movimiento de los vórtices en la convección térmica giratoria se asemejaba a las partículas inerciales que realizaban el movimiento browniano. El movimiento experimentó una transición brusca de las regiones balísticas a las difusivas sin experimentar una región de memoria hidrodinámica intermedia. La observación del movimiento browniano puro fue predicha por primera vez por Paul Langevin, aunque no se había observado previamente en la práctica para partículas inerciales en sistemas líquidos. El trabajo destacó el trabajo teórico clásico existente que mostró cómo las trazas pasivas exhibieron una transición de comportamiento balístico a difusivo, similar a las observaciones experimentales de este estudio. El movimiento browniano puro observado también indicó la insignificancia del efecto de memoria hidrodinámica. Chong y col. consideró la fuerza de Coriolis durante el estudio debido a su relevancia en la formación de vórtices en los fenómenos naturales, incluyendo ciclones tropicales en la atmósfera, vórtices oceánicos y la mancha roja gigante de larga duración en Júpiter. Los hallazgos influirán en muchas situaciones en astrofísica, geofísica y meteorología.
© 2020 Science X Network