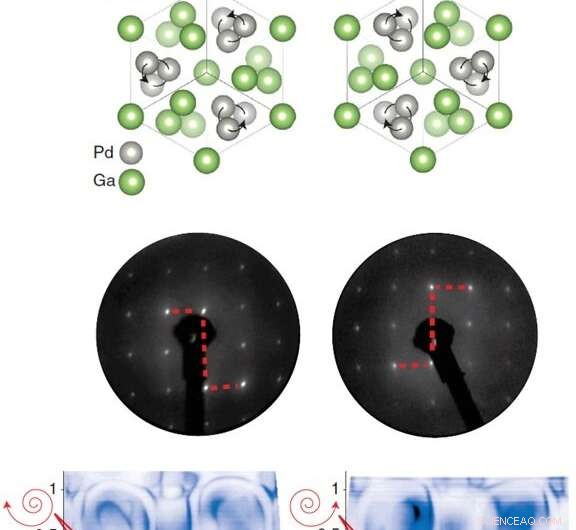
Los cristales de PdGa se pueden cultivar con dos quiralidades estructurales distintas (columna izquierda y derecha). Los dos enantiómeros tienen estructuras cristalinas espejadas (segunda fila), como se ve en los patrones de reflexión de electrones (tercera fila). Schröter y col. ahora demuestre que la destreza se refleja también en la estructura de las superficies Fermi (fila inferior), que determinan el comportamiento electrónico del material. Ambos compuestos muestran el número máximo de Chern, pero con signo opuesto, +4 y -4, respectivamente. (Adaptado de la ref. 1.) Crédito:Paul Scherrer Institute / Niels Schröter
En materiales topológicos, Los electrones pueden mostrar un comportamiento que es fundamentalmente diferente al de la materia 'convencional', y la magnitud de muchos de esos fenómenos "exóticos" es directamente proporcional a una entidad conocida como número de Chern. Nuevos experimentos establecen por primera vez que el número máximo de Chern predicho teóricamente se puede alcanzar, y controlar, en un material real.
Cuando la Real Academia Sueca de Ciencias otorgó el Premio Nobel de Física 2016 a David Thouless, Duncan Haldane y Michael Kosterlitz, alabaron al trío por haber "abierto la puerta a un mundo desconocido donde la materia puede asumir estados extraños". Lejos de ser una rareza, los descubrimientos de las transiciones de fase topológica y las fases topológicas de la materia, a lo que los tres teóricos han contribuido de manera tan crucial, se ha convertido en uno de los campos de investigación más activos de la física de la materia condensada en la actualidad. Los materiales topológicos mantienen la promesa, por ejemplo, para dar lugar a nuevos tipos de componentes electrónicos y superconductores, y albergan conexiones profundas entre áreas de la física y las matemáticas.
Si bien se descubren nuevos fenómenos de forma rutinaria, hay aspectos fundamentales aún por resolver. Uno de ellos es cuán 'fuertes' pueden ser los fenómenos topológicos en un material real. Respondiendo a esa pregunta, un equipo internacional de investigadores dirigido por el investigador postdoctoral de la ISP Niels Schröter proporciona ahora un importante punto de referencia. Escribiendo en Ciencias , reportan experimentos en los que observaron que en el semimetal topológico paladio galio (PdGa) uno de los clasificadores más comunes de fenómenos topológicos, el número de Chern, puede alcanzar el valor máximo permitido en cualquier cristal metálico. Nunca antes se había demostrado que esto sea posible en un material real. Es más, el equipo ha establecido formas de controlar el signo del número de Chern, lo que podría traer nuevas oportunidades para explorar, y explotando, Fenómenos topológicos.
Desarrollado al máximo
En trabajos teóricos se había predicho que en semimetales topológicos el número de Chern no puede exceder una magnitud de cuatro. Como sistemas candidatos que muestran fenómenos con números de Chern máximos, Se propusieron cristales quirales. Estos son materiales cuyas estructuras de celosía tienen una mano bien definida, en el sentido de que no pueden transformarse en su imagen especular mediante ninguna combinación de rotaciones y traslaciones. Se han estudiado varias estructuras candidatas. Una observación experimental concluyente de un número de Chern de más o menos cuatro, sin embargo, permaneció esquivo. Los esfuerzos anteriores se han visto obstaculizados por dos factores en particular. Primero, un prerrequisito para realizar un número de Chern máximo es la presencia de acoplamiento espín-órbita, y al menos en algunos de los materiales estudiados hasta ahora, ese acoplamiento es relativamente bajo, dificultando la resolución de las divisiones de interés. Segundo, preparar superficies limpias y planas de cristales relevantes ha sido un gran desafío, y como consecuencia, las firmas espectroscópicas tendían a desaparecer.
Schröter y col. han superado estas dos limitaciones trabajando con cristales de PdGa. El material muestra un fuerte acoplamiento de giro-órbita, y existen métodos bien establecidos para producir superficies inmaculadas. Además, en la línea de luz de Espectroscopias Resonantes Avanzadas (ADRESS) de Swiss Light Source en PSI, tenían capacidades únicas a su disposición para experimentos ARPES de alta resolución y, por lo tanto, para resolver los patrones espectroscópicos reveladores predichos. En combinación con otras mediciones en Diamond Light Source (Reino Unido) y con cálculos ab initio dedicados, estos datos revelaron firmas duras y rápidas en la estructura electrónica de PdGa que no dejaron ninguna duda de que se ha realizado el número máximo de Chern.
Una mano en el número de Chern
El equipo dio un paso más, más allá de la observación de un número máximo de Chern. Demostraron que la naturaleza quiral de los cristales de PdGa también ofrece la posibilidad de controlar el signo de ese número. Para demostrar tal control, cultivaron muestras que eran zurdas o diestras (ver la figura). Cuando miraron las estructuras electrónicas de los dos enantiómeros, encontraron que la quiralidad de los cristales se refleja en la quiralidad de la función de onda electrónica. Tomados en conjunto, esto significa que en los semimetales quirales la mano, que se puede determinar durante el crecimiento de los cristales, Puede utilizarse para controlar los fenómenos topológicos que surgen del comportamiento de los electrones en el material. Este tipo de control abre un tesoro de nuevos experimentos. Por ejemplo, Se puede esperar que surjan nuevos efectos en la interfaz entre diferentes enantiómeros, uno con el número Chern +4 y el otro con -4. Y existen perspectivas reales de solicitudes, también. Los semimetales topológicos quirales pueden albergar fenómenos fascinantes como las fotocorrentes cuantificadas. Curiosamente, PdGa es conocido por sus propiedades catalíticas, invitando a la pregunta sobre el papel de los fenómenos topológicos en tales procesos.
Finalmente, Los hallazgos ahora obtenidos para PdGa surgen de las propiedades de las bandas electrónicas que son compartidas por muchos otros compuestos quirales, lo que significa que el rincón del "mundo desconocido donde la materia puede asumir estados extraños" en el que Schröter y sus colegas ahora se han aventurado probablemente tenga mucho más para ofrecer.