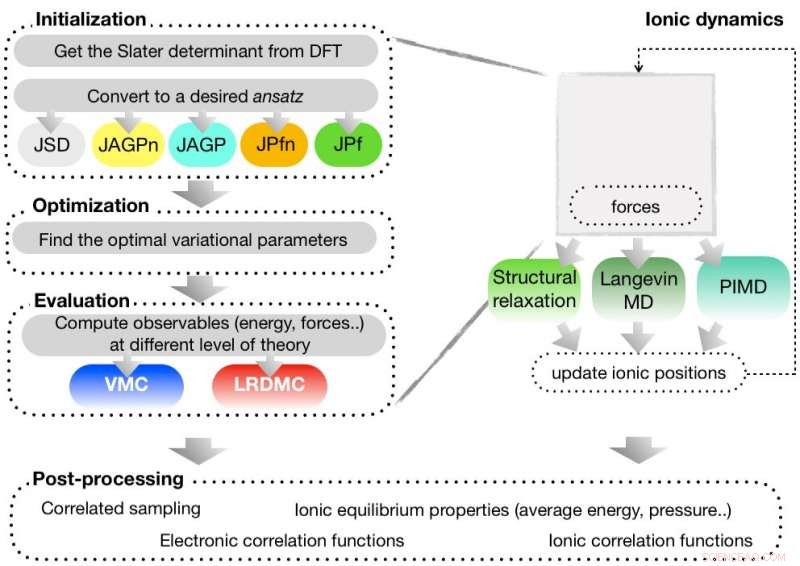
Figura esquemática del flujo de trabajo TurboRVB [K. Nakano y col. J. Chem. Phys. 152, 204121 (2020)]. El código implementa la función de onda flexible de muchos cuerpos ansatz, como JSD:Jastrow Slater, JAGP:Jastrow Geminal, y JPf:Jastrow Pfaffian. Se puede preparar una función de onda de prueba utilizando un código de teoría funcional de densidad (DFT) incorporado y realizar cálculos posteriores de Monte Carlo cuántico variacional (VMC) de los primeros principios y de Monte Carlo cuántico de difusión discretizada de celosía (LRDMC). Dado que se pueden calcular las fuerzas que actúan sobre los átomos, Las optimizaciones estructurales y las simulaciones de dinámica molecular también son factibles en TurboRVB. Crédito:Publicaciones AIP
El Monte Carlo cuántico de primeros principios es un marco utilizado para abordar la solución de la ecuación de Schrödinger de muchos cuerpos mediante un enfoque estocástico. Se espera que este marco sea la próxima generación de cálculos de estructuras electrónicas porque puede superar algunos de los inconvenientes de la teoría funcional de la densidad y los cálculos basados en funciones de onda. En particular, el marco cuántico de Monte Carlo no se basa en funciones de correlación de intercambio, el algoritmo es adecuado para supercomputadoras masivamente paralelas, y es fácilmente aplicable tanto a sistemas aislados como periódicos.
TurboRVB es un paquete de software de Monte Carlo cuántico de primeros principios que fue lanzado inicialmente por el profesor Sandro Sorella (Escuela Internacional de Estudios Avanzados / Italia) y el Dr. Michele Casula (Universidad de la Sorbona / Francia). y ha sido desarrollado continuamente por muchos colaboradores durante más de 20 años. Muy recientemente, Ayudar. El profesor Kosuke Nakano del Instituto Avanzado de Ciencia y Tecnología de Japón (JAIST, Presidente:Minoru Terano, ubicado en Nomi, Ishikawa, Japón) y sus colaboradores han publicado un artículo de revisión completo en el Revista de física química .
TurboRVB se distingue de otros códigos de Monte Carlo cuánticos de primeros principios en las siguientes características. (a) El código emplea funciones de onda de tipo enlace de valencia resonante (RVB), como Jastrow Geminal / Jastrow Pfaffian, que incluyen el efecto de correlación más allá de la función de onda Jastrow-Slater que se usa comúnmente en otros códigos QMC. (b) Implementa algoritmos de optimización de última generación, como la reconfiguración estocástica y el método lineal, ayuda a realizar una optimización estable de la amplitud y la superficie nodal de una función de onda de muchos cuerpos en el nivel de Monte Carlo cuántico variacional. (c) El llamado método Monte Carlo de difusión regularizada en celosía se implementa en el código, que proporciona un cálculo de Monte Carlo cuántico de difusión numéricamente estable. (d) La implementación de una diferenciación algorítmica adjunta nos permite calcular derivadas de funciones de onda de muchos cuerpos de manera muy eficiente y realizar optimizaciones estructurales y simulaciones de dinámica molecular.