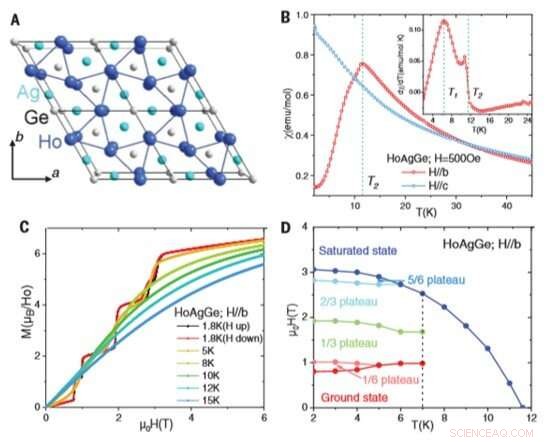
Estructura cristalina y propiedades magnéticas de HoAgGe. (A) Proyección del eje c de la estructura cristalina de HoAgGe, con la definición de las direcciones ay b. (B) Susceptibilidad a baja temperatura c (T) de HoAgGe para H // by H // c por debajo de 500 Oe, con dc (T) / dT en el recuadro. (C) Magnetización isotérmica en el plano (H // b) para HoAgGe a varias temperaturas. (D) Dependencia de las transiciones metamagnéticas de la temperatura, con la línea de puntos que indica Crédito T1:Ciencia, doi:10.1126 / science.aaw1666
Las fases exóticas de la materia conocidas como hielos de espín se definen por giros frustrados que obedecen a las "reglas del hielo" locales, similares a los dipolos eléctricos en el hielo de agua. Los físicos pueden definir reglas de hielo en dos dimensiones para giros en el plano similares a los de Ising dispuestos en una red de kagome. Las reglas del hielo pueden dar lugar a diversos órdenes y excitaciones. En un nuevo informe sobre Ciencias , Kan Zhao y un equipo de física experimental, cristalografía, y materiales e ingeniería en Alemania, y la República Checa utilizaron enfoques experimentales y teóricos, incluida la magnetometría, termodinámica, dispersión de neutrones y simulaciones de Monte Carlo para establecer el cristal HoAgGe como un sistema cristalino para realizar el exótico estado de hielo de espín de kagome. La configuración presentaba una variedad de estados parcial y totalmente ordenados, así como fases inducidas por el campo a bajas temperaturas consistentes con los requisitos experimentales de kagome.
La formación de fases exóticas de la materia puede causar frustraciones en los sistemas de espín. Por ejemplo, las restricciones locales en una molécula pueden conducir a un número macroscópico de estados fundamentales degenerados oa un estado fundamental extenso en entropía. En configuraciones bidimensionales, Las reglas del hielo requieren elaborados arreglos de giros en celosías kagome de forma triangular. Como consecuencia, los hielos de espín de kagome mostraron un comportamiento de ordenación en múltiples etapas bajo temperatura cambiante. Hasta ahora, los físicos solo habían realizado experimentalmente hielos de espín de kagome en sistemas de hielo de espín artificial formados por nanobarras de ferromagnetos organizados en redes de panal de abejas. En este trabajo. Zhao y col. utilizó múltiples enfoques experimentales y teóricos para demostrar el compuesto intermetálico HoAgGe como un hielo de espín kagome existente de forma natural con un estado fundamental completamente ordenado.

Estructuras magnéticas de HoAgGe versus temperatura y campo con H // b. (A) Intensidad integrada del pico magnético (1/3, 1/3, 0) de 13 K a 3,8 K según la difracción de neutrones, con la intensidad integrada del emplazamiento nuclear (1, 0, 0) como un recuadro. (B) Estructuras magnéticas refinadas de HoAgGe a 10 K. La celda unitaria magnética está indicada por el rombo verde, con los tres sitios Ho desiguales Ho1, Ho2, y Ho3 etiquetado con 1, 2, y 3, respectivamente, para simplificar. (C) Hexágonos de espines en sentido antihorario en la estructura parcialmente ordenada de HoAgGe a 10 K, con 1/3 de giros que no participan en la orden de largo alcance. (D) Intensidad integrada del pico magnético (–1/3, 2/3, 1) y (1/3, 4/3, 1) versus campo a 4 K. (E) Estructura magnética refinada de HoAgGe a 4 K. (F) Hexágonos de espines en sentido horario y antihorario en la estructura magnética de HoAgGe a 4K, que es exactamente el estado fundamental √3 × √3 esperado de kagome spin ice. (G) Estructura magnética refinada de HoAgGe en H =1.5 T y T =4 K. El refinamiento se realizó en el rectángulo verde claro de 3 × √3. Los seis sitios Ho desiguales están etiquetados con números del 1 al 6 para simplificar. (H) Estructura magnética refinada de HoAgGe en H =2.5 T y T =1.8 K. (I) Estructura magnética refinada de HoAgGe en H =4 T y T =1.8 K, con los dos sitios Ho desiguales etiquetados con 1 y 2. La dirección del campo está marcada por la flecha roja para (G) a (I). Crédito:Ciencia, doi:10.1126 / science.aaw1666
Luego, el equipo realizó mediciones de estructura y magnetometría de HoAgGe. Aunque las mediciones de difracción de neutrones realizadas en el pasado sugirieron estructuras magnéticas no colineales de HoAgGe, estos experimentos se basaron en muestras de polvo que eran insuficientes para determinar completamente la estructura magnética en presencia de frustración. Zhao y col. combinó la difracción de neutrones con mediciones termodinámicas en HoAgGe monocristalino para mostrar sus exóticas estructuras magnéticas dependientes de la temperatura y el campo magnético, en consonancia con la regla del hielo de kagome. Para determinar completamente las estructuras magnéticas a partir de la difracción de neutrones basadas en estructuras de espín no triviales de HoAgGe, Zhao y col. realizó experimentos de difracción de neutrones monocristalinos, hasta 1,8 K. Por debajo de una transición de alta temperatura a 11,6 K, el equipo observó un pico magnético.
Cuando refinaron los datos de neutrones a 4 K, el equipo observó una estructura magnética más detallada donde el estado fundamental completamente ordenado indicaba giros hexagonales alternados en sentido horario y antihorario. El estado fundamental √3 x √3 resultante representaba con precisión el hielo de espín de kagome clásico, como se predijo teóricamente. De acuerdo con la regla de hielo de Kagome, el acoplamiento ferromagnético dominante del vecino más cercano debe ocurrir entre espines coplanar con anisotropía uniaxial similar a Ising dependiente del sitio. En el presente trabajo, Zhao y col. anisotropía similar a Ising calculada y confirmada del campo eléctrico cristalino (CEF) para los cristales de HoAgGe.
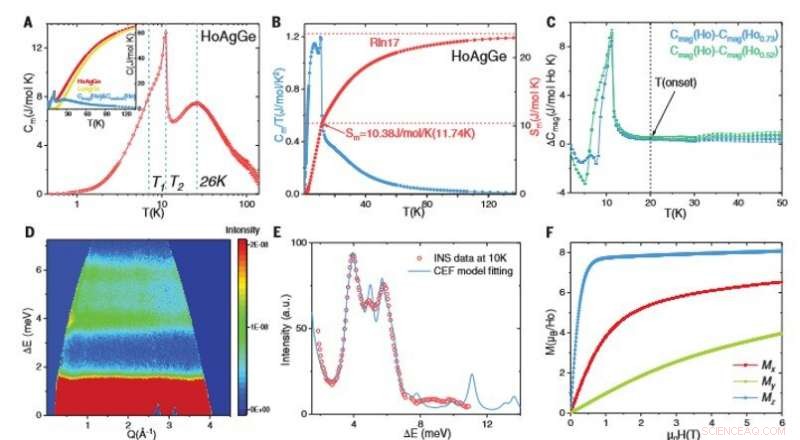
Calor magnético específico y resultados INS de HoAgGe. (A) Contribución magnética al calor específico Cm de HoAgGe con las líneas punteadas que indican T1, T2, y un pico ancho a 26 K. Tenga en cuenta que las barras de error por debajo de 30 K son más pequeñas que los tamaños de los símbolos. (Recuadro) Calor específico de HoAgGe, LuAgGe, y su diferencia. Este último se define como la suma de las contribuciones magnéticas y nucleares al calor específico de HoAgGe. (B) Datos Cm / T y la correspondiente entropía magnética Sm, que se acerca al valor teórico de Rln17 por encima de 100 K. (C) Diferencia entre el calor específico magnético de HoAgGe y el de Lu1-xHoxAgGe (x =0.52 y 0.73) después de la normalización (ver texto). (D) Espectros INS de HoAgGe a 10 K con longitud de onda del neutrón incidente 3 Å. (E) Cortes de Q constante (1.4
Para confirmar aún más la autenticidad de HoAgGe como un spin ice de kagome, el equipo de investigación investigó si las reglas de hielo establecidas eran aplicables incluso fuera del estado fundamental completamente ordenado. Usando difracción de neutrones bajo campos magnéticos, mostraron que HoAgGe cumplía con estos requisitos y observaron un campo magnético creciente con cambios repentinos durante las transiciones metamagnéticas. Para mayor información, Zhao y col. refinó las estructuras magnéticas obtenidas de la dispersión de neutrones y señaló las transiciones magnéticas que resultan de la competencia entre el campo magnético externo y acoplamientos más débiles que no afectan la regla del hielo.
Después de establecer que la regla del hielo de kagome se aplicaba a los cristales de HoAgGe a baja temperatura, el equipo examinó los comportamientos termodinámicos del hielo de espín de kagome aislando la contribución magnética al calor específico deduciendo las contribuciones de los núcleos, vibraciones reticulares y electrones itinerantes del cristal. Para determinar hasta qué punto los espines Ho iónicos del cristal HoAgGe podrían verse aproximadamente como Ising, Zhao y col. A continuación se analizan los efectos del campo eléctrico cristalino (CEF). Para comprender directamente la división de CEF, llevaron a cabo experimentos de dispersión de neutrones inelásticos (INS) de cristales de HoAgGe utilizando el espectrómetro de tiempo de vuelo avanzado. Los resultados indicaron cuatro modos CEF de baja energía que mostraban anisotropía de tipo Ising.
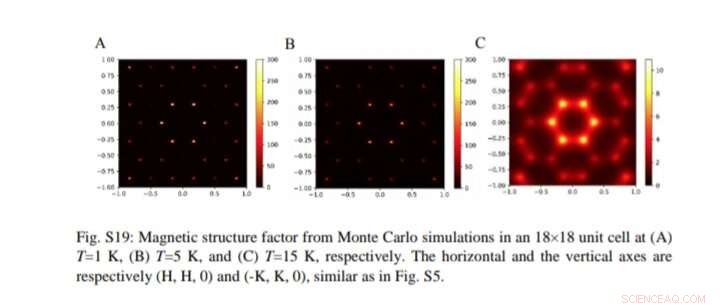
Factor de estructura magnética de la simulación de Monte Carlo en una celda unitaria de 18 x 18 a (A) T =1 K, (B) T =5 K y (C) T =15 K. Los ejes horizontal y vertical fueron respectivamente (H, H 0) y (-K, K, 0). Crédito:Ciencia, doi:10.1126 / science.aaw1666
Basado en la evidencia experimental, propusieron un modelo de espín clásico que contiene espines en plano similares a los de Ising en una red de kagome distorsionada en 2-D. Usando simulaciones de Monte Carlo del modelo de espín clásico en una celosía de 18 x 18, reprodujeron el estado fundamental y el estado parcialmente ordenado para capturar el modelo de espín clásico y las principales características del magnetismo HoAgGe a bajas temperaturas. El modelo desarrollado en el estudio difería de los casos de hielo kagome dipolares y de corto alcance en relación con los acoplamientos de intercambio y las interacciones dipolares de largo alcance. con investigaciones adicionales que requieren un estudio por separado.
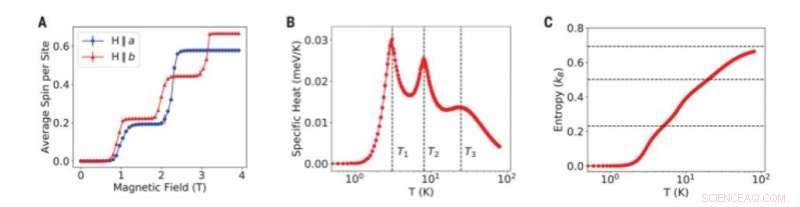
Simulaciones de Monte Carlo del modelo de espín clásico 2D para HoAgGe. (A) M (H) curvas a 1 K para H a lo largo de los ejes ayb. (B) Dependencia de la temperatura del calor específico por giro. (C) Entropía magnética por giro calculada a partir del calor específico. Las tres líneas horizontales discontinuas corresponden a ln2 ≈ 0.693 (Ising paramagnético), 0.501 (orden de hielo de corto alcance), y 1 3ln2≈0:231 (orden toroidal), respectivamente. Se utilizó una celda de 18 × 18 para el cálculo. Crédito:Ciencia, doi:10.1126 / science.aaw1666
De este modo, las simulaciones de Monte Carlo del modelo de espín clásico sólo coincidieron parcialmente con los experimentos. La discrepancia puede haber resultado de múltiples, niveles bajos de CEF del Ho 3+ iones. En HoAgGe, la metalicidad suprimió simultáneamente la división CEF de Ho 3+ iones para mejorar el acoplamiento de intercambio entre ellos, haciendo que las dos escalas de energía sean comparables a los niveles bajos de CEF. El modelo semiclásico resultante todavía se puede asignar a un modelo de Ising, explicando así la validez del experimento. En comparación con otros hielos de pirocloro, la naturaleza metálica de HoAgGe lo convirtió en un hielo kagome de alta temperatura y también puede conducir a más fenómenos exóticos, incluyendo interacciones entre corrientes eléctricas y monopolos magnéticos, así como efectos magnetoeléctricos metálicos.
© 2020 Science X Network