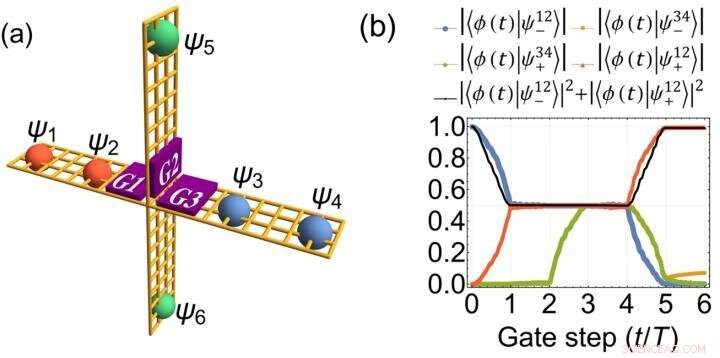
(a) Unión en forma de cruz basada en nanocables que soporta el trenzado no abeliano de los modos cero Jackiw-Rebbi. (b) Resultados numéricos para la evolución de la función de onda que demuestra las propiedades de trenzado no abeliano de los modos cero Jackiw-Rebbi. Crédito:© Science China Press
Como rama importante de la computación cuántica, La computación cuántica topológica ha atraído una gran atención por tener grandes ventajas como la tolerancia a fallas. La computación cuántica topológica se basa en el trenzado no abeliano de estados cuánticos, donde el trenzado no abeliano en el campo de la estadística cuántica está altamente relacionado con la no localidad de los estados cuánticos. La exploración de la computación cuántica topológica en las últimas dos décadas se centra principalmente en el fermión de Majorana (o su encarnación de energía cero conocida como modo cero de Majorana), una partícula exótica que posee estadísticas no abelianas y es bien conocida por ser ella misma como antipartícula.
El modo cero de Jackiw-Rebbi se planteó por primera vez en el campo de la física de altas energías en la década de 1970. Con la creciente importancia de la topología en el área de la física de la materia condensada, También se adoptó el concepto de modo cero Jackiw-Rebbi para referirse al modo cero protegido topológicamente en el límite de los aislantes topológicos. En contraste con el modo cero de Majorana que solo se presenta con un parámetro de orden superconductor que no desaparece, El modo cero de Jackiw-Rebbi no es auto-conjugado y, por lo tanto, podría presentarse incluso en ausencia de simetría entre partículas y agujeros.
Recientemente, en un artículo de investigación titulado "Efecto Aharonov-Bohm de doble frecuencia y propiedades de trenzado no abeliano del modo cero Jackiw-Rebbi, " publicado en Revista Nacional de Ciencias , Investigadores de cuatro universidades, incluidas la Universidad de Pekín y la Universidad de Xi'an Jiaotong, afirmaron un nuevo método que realiza el trenzado no abeliano. Coautores Yijia Wu, Haiwen Liu, Jie Liu, Hua Jiang, y X. C. Xie demostró que los modos cero Jackiw-Rebbi que existen ampliamente en los aisladores topológicos también admiten el trenzado no abeliano.
En este trabajo, los autores construyeron modos cero Jackiw-Rebbi en un aislador Hall de espín cuántico. Al mostrar la frecuencia de oscilación Aharonov-Bohm del transporte intermedio de modo cero Jackiw-Rebbi se duplica, afirmaron que el modo cero de Majorana puede verse como un caso especial del modo cero Jackiw-Rebbi con simetría de agujeros de partículas. En el método de simulación numérica, También demostraron que los modos cero de Jackiw-Rebbi exhiben propiedades de trenzado no abeliano en ausencia de superconductividad. Los autores creían que estos resultados no solo hacen un progreso teórico que exhibe las encantadoras propiedades del modo cero de Jackiw-Rebbi, pero también brindan la posibilidad de realizar computación cuántica topológica en un sistema no Majorana (sin superconductividad).
Esta última investigación también presentó una regla de fusión generalizada y continuamente sintonizable en el cálculo cuántico topológico cuando se levanta la degeneración de los modos cero Jackiw-Rebbi. Los autores concluyeron que el modo cero de Jackiw-Rebbi podría ser un nuevo candidato para el cálculo cuántico topológico y tiene ventajas adicionales en comparación con su primo Majorana:(1) la superconductividad ya no es necesaria; (2) posee una regla de fusión generalizada; y (3) la brecha energética es generalmente mayor.