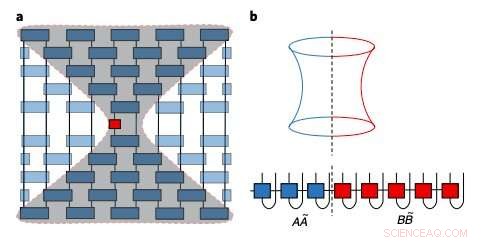
Bosquejo del cono de luz emergente y la estructura de entrelazamiento de los operadores locales de Heisenberg en formas de red tensorial. Crédito:Xu &Swingle.
En física cuántica, la codificación es la dispersión de información cuántica a través de un sistema cuántico complejo, como los caóticos sistemas cuánticos de muchos cuerpos. Este proceso puede dificultar o imposibilitar el acceso a la información cuántica, particularmente cuando se utilizan métodos físicos simples y convencionales.
La codificación se puede medir utilizando correlacionadores ordenados fuera de tiempo (OTOC), que son medidas de caos cuántico ligadas al crecimiento de los operadores de Heisenberg. Investigadores de la Universidad de Maryland han introducido recientemente un nuevo método para calcular las OTOC de los operadores locales en sistemas 1-D. Este método, presentado en un artículo publicado en Física de la naturaleza , En última instancia, podría usarse para estudiar la codificación en sistemas cuánticos complejos.
"El problema básico que estábamos tratando de comprender es cómo se propaga el caos en el espacio en los sistemas cuánticos, "Brian Swingle, uno de los investigadores que realizó el estudio, dijo Phys.org. "Piense en el experimento mental del efecto mariposa. Queríamos saber:si una mariposa agita sus alas, ¿Qué tan rápido se propaga esa perturbación en el espacio? Queríamos entender esto específicamente en el contexto de los sistemas cuánticos compuestos por muchas partículas ".
Estudios anteriores que investigaron cómo se propaga el caos en el espacio dentro de los sistemas cuánticos reunieron varias observaciones interesantes, pintando un paisaje interesante pero bastante complejo de posibles comportamientos. Muchos de estos estudios, sin embargo, se basaron en supuestos especiales y esto hace que sea más difícil determinar en qué medida sus conclusiones pueden generalizarse a otros sistemas.
En su estudio, Swingle y su colega Shenglong Xu se propusieron investigar qué comportamientos revelados en estudios anteriores son genéricos para todos los sistemas cuánticos. También esperaban comprender cómo se puede pensar en el panorama de posibilidades que ocurren en diferentes sistemas especiales.
"Para saber cuál era el comportamiento genérico, necesitábamos un método para calcular OTOC en sistemas genéricos, "Dijo Swingle." Tal método necesitaría utilizar alguna propiedad genérica de las OTOC en los sistemas locales ".
La idea de los investigadores era utilizar la propiedad de cono de luz de los sistemas cuánticos, lo que implica que fuera del cono expansivo de influencia que surge del aleteo metafórico de la mariposa, el sistema apenas se perturba. En otras palabras, fuera del "cono de mariposa", el efecto de la mariposa sigue siendo pequeño.
En mecánica cuántica, las acciones se representan como operadores y la pequeñez de un efecto dado se traduce en la sencillez del operador. Aprovechando esta simplicidad, Swingle y Xu pudieron representar al operador de una manera computacionalmente útil (es decir, como 'operador de producto matricial'), para realizar los cálculos necesarios para acceder al cifrado.
"Hay dos logros clave en nuestro estudio, "Swingle dijo." Primero, ideamos un marco teórico para clasificar varios comportamientos posibles de la OTOC. Este marco era lo suficientemente general como para incluir todos los ejemplos conocidos anteriormente. Segundo, formulamos un método de propósito general para calcular las OTOC, un método que podría ir más allá de los cálculos anteriores ".
Swingle y Xu ya han utilizado su método para calcular las OTOC de los operadores locales para estudiar una variedad de sistemas genéricos. Curiosamente, encontraron que varios de estos sistemas encajan en su marco teórico. En un estudio de seguimiento presentado en Revisión física X , los investigadores también utilizaron su método para recopilar evidencia de que las OTOC en sistemas caóticos genéricos tienen un comportamiento universal.
"Hemos seguido este trabajo aplicando nuestra tecnología a varios sistemas diferentes que se están estudiando en experimentos de sobremesa en todo el mundo, ", Dijo Swingle." Ahora también estamos generalizando el enfoque para incluir nuevos tipos de efectos, incluido el estudio de sistemas a baja temperatura donde la velocidad de propagación del caos tiende a disminuir ".
© 2019 Science X Network