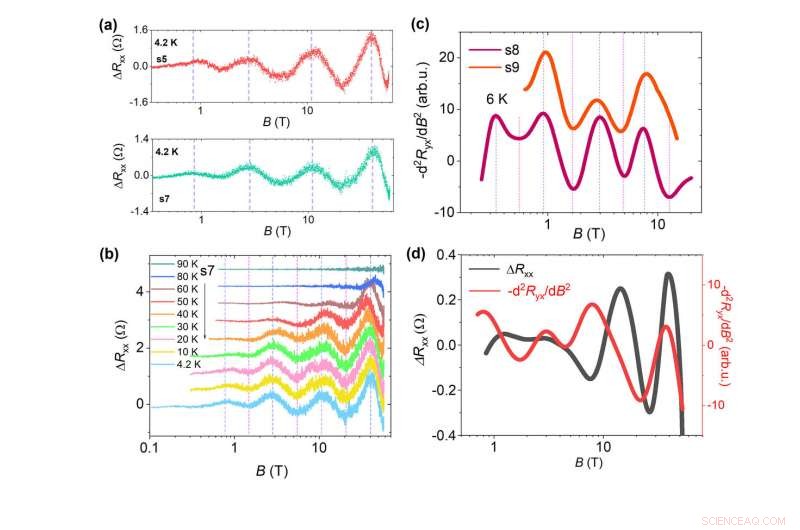
(a) Oscilaciones de MR log-periódicas en HfTe5 después de restar el fondo. (b) Dependencia de la temperatura de las oscilaciones periódicas logB. (c) Señales de oscilaciones periódicas logB en las trazas de Hall de HfTe5. (d) Comparación de las oscilaciones en los trazos de MR y Hall para la misma muestra. Crédito:© Science China Press
Un problema fundamental de la electrodinámica cuántica es el destino del núcleo atómico superpesado, que se propone colapsar cuando el número atómico excede cierto valor. Sin embargo, este intrigante fenómeno de colapso supercrítico sigue siendo esquivo en los experimentos. La invariancia de escala discreta (DSI) es una anomalía de escala con la violación de la simetría de escala continua. La intrigante log-periodicidad es la firma característica de DSI, que existe en ruptura, procesos de crecimiento, turbulencia, Finanzas, etcétera. La función DSI es de gran interés en física cuántica, mientras que rara vez se puede realizar experimentalmente en sistemas cuánticos. El ejemplo previamente conocido con DSI en física cuántica solo se enfoca en el estado del trímero de Efimov.
Se ha observado un nuevo tipo de oscilaciones cuánticas de magnetorresistencia en el material topológico ZrTe. 5 (Science Advances 4, eaau5096 (2018)), constituyendo el tercer tipo distintivo conocido de periodicidad en los casi 90 años de búsqueda de oscilaciones cuánticas en sólidos. Es más, El descubrimiento de las oscilaciones periódicas logB exóticas puede representar virtualmente la invariancia de escala discreta asociada con los estados cuasi ligados formados a través del colapso atómico supercrítico en materiales de Dirac. Se supone que esta característica peculiar es universal en los materiales de Dirac con atracción de Coulomb. Por lo tanto, es deseable extender las investigaciones a otros sistemas topológicos, y más importante a otros observables físicos. En un nuevo trabajo publicado en el Revista Nacional de Ciencias , Colaboración de investigación con sede en Beijing dirigida por el profesor Jian Wang, El profesor Haiwen Liu y el profesor Jiyan Dai han revelado la universalidad de las magneto-oscilaciones cuánticas log-periódicas y el fenómeno DSI en materiales de Dirac mediante los resultados de magneto-transporte de HfTe. 5 cristales.
Los científicos midieron la resistencia magneto y Hall del HfTe 5 cristales en campos magnéticos pulsados hasta 58 T y campos magnéticos estáticos hasta 25 T. Se observan oscilaciones cuánticas claras logB-periódicas que señalan DSI en la magnetorresistencia longitudinal (MR) (subfigura (a)), independiente de las diferencias menores de la calidad de la muestra. La dependencia de la temperatura de las oscilaciones periódicas logB en HfTe5 se muestra en la subfigura (b). Se puede ver que las características log-periódicas se vuelven invisibles cuando se aumenta la temperatura por encima de 80 K. Además, por primera vez, la señal DSI con una notable periodicidad logB se descubre en las trazas de Hall de los cristales de HfTe5. El hallazgo indica un efecto general de la función DSI en las propiedades de transporte del sistema. Los segundos resultados derivados de los datos de Hall se muestran en la subfigura (c). Además, los resultados de MR y Hall en la misma muestra se muestran en la subfigura (d). Se encuentra que en las oscilaciones la fase de los datos de Hall está ligeramente por delante de MR, recuerda a eso en el efecto Hall cuántico bidimensional.
Las oscilaciones logarítmicas periódicas en los materiales de Dirac se atribuyeron al fenómeno de colapso atómico supercrítico y los estados cuasi ligados concomitantes que presentan invariancia de escala discreta en los materiales de Dirac. La cuasi-partícula en los materiales de Dirac obedece a la ecuación relativista, y la velocidad de Fermi es mucho menor que la velocidad de la luz en el vacío. Por lo tanto, el valor de la constante de estructura fina en los materiales de Dirac es mucho mayor que en el vacío, que proporciona una plataforma prometedora para investigar el fenómeno del colapso atómico supercrítico. Debido al gran valor de la constante de estructura fina en estos sistemas de estado sólido, la atracción de Coulomb da lugar al colapso atómico supercrítico en analogía al fenómeno propuesto para existir en átomos superpesados. Es más, la ecuación de Dirac sin masa con atracción de Coulomb conserva la invariancia de escala discreta, en contraste con la simetría de escala discreta que se rompe en la ecuación de Dirac masiva de átomos superpesados.
En material topológico HfTe5, las oscilaciones cuánticas logarítmicas periódicas tanto en la RM longitudinal como en la resistencia de Hall están estrechamente relacionadas con los estados cuasi ligados de las partículas de Weyl de la banda de huecos con atracción de Coulomb de largo alcance cuando la densidad del portador está tan diluida, y la atracción de Coulomb de largo alcance es generada por la impureza de carga o el tipo opuesto de portadores. Aparte de los estados cuasi limitados cerca del centro de Coulomb, También existe un gran número de operadores de telefonía móvil en la superficie de Fermi. Por lo tanto, la dispersión resonante entre los portadores móviles y los estados cuasi enlazados alrededor del nivel de Fermi determinan las propiedades de transporte del material, p.ej. el MR longitudinal y los trazos de Hall. Un análisis teórico adicional significa que el cambio de fase π / 2 se origina en la dispersión resonante entre los operadores móviles y los estados cuasi enlazados, compartiendo el mismo origen de las oscilaciones log-periódicas. Es más, Los científicos han analizado la influencia de una pequeña banda prohibida en la función DSI y han aclarado su relevancia para varios materiales topológicos.
Los materiales de Dirac que muestran una periodicidad logarítmica proporcionan plataformas prometedoras para investigar el fenómeno de colapso atómico supercrítico raramente observado y la característica de invariancia de escala discreta. Este trabajo proporciona nuevos conocimientos para comprender mejor la universalidad y la naturaleza física de las oscilaciones cuánticas logarítmicas periódicas en los materiales de Dirac.