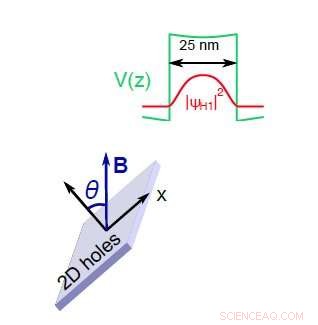
Agujero cuántico superior derecho de GaAs bien utilizado en el estudio. Abajo a la izquierda:el dispositivo está inclinado en ángulo con respecto al campo magnético aplicado. Crédito:FLOTA
Los 'giros' de electrones (y huecos) en semiconductores tienen aplicaciones potenciales en espintrónica, computación cuántica basada en espines, y sistemas topológicos.
El giro de una partícula es su momento angular intrínseco.
En un campo magnético, los giros de los electrones o agujeros se orientan en paralelo ('giro hacia arriba') o antiparalelo ('giro hacia abajo') a la dirección del campo, como la aguja de una brújula.
Estas orientaciones paralelas y antiparalelas tienen diferentes energías, y es esta diferencia de energía (conocida como división de Zeeman si es causada por un campo magnético) la que tiene la clave para el procesamiento de información basado en espines.
En un artículo publicado esta semana, Los investigadores de FLEET en la UNSW han demostrado un mecanismo completamente nuevo para controlar eléctricamente el giro de los agujeros en un pozo cuántico. El documento aparece esta semana en Física APS .
Los agujeros son cuasipartículas, básicamente 'electrones faltantes', un poco como la burbuja en un nivel de burbuja, la silla perdida en un juego de sillas musicales, o el jugador faltante en una línea defensiva. ¿Suena un poco esotérico? Bien, la mitad de los transistores en su computadora portátil o iPhone en realidad cambian usando el movimiento de 'agujeros' cargados positivamente, en lugar de electrones cargados negativamente.
Entonces, ¿dónde encaja el giro en el rompecabezas? Para responder a esto, uno necesita hacer zoom en la imagen atómica. En un átomo la interacción espín-órbita acopla el giro de los electrones (o huecos) a su movimiento alrededor del núcleo del átomo. Debido a este acoplamiento, los electrones (o huecos) en movimiento 'perciben' el campo eléctrico del núcleo como un campo magnético efectivo, lo que luego hace que los electrones (o huecos) tengan dos orientaciones de espín opuestas con una diferencia de energía, una analogía de la división de Zeeman.

Autora principal, Dra. Elizabeth Marcellina. Crédito:FLOTA
Pero esa no es toda la historia:los agujeros tienen propiedades de giro muy diferentes a las de los electrones. A diferencia de los electrones, que son partículas de 1/2 espín, los agujeros en los semiconductores son cuasipartículas de giro 3/2. Esta diferencia de giro significa que los agujeros reaccionan de manera bastante diferente a un campo eléctrico o un campo magnético.
La interacción espín-órbita en los huecos es mucho más fuerte que en los electrones, lo que significa que la diferencia de energía entre dos orientaciones de espín opuestas es mucho mayor y mucho más sensible a los campos eléctricos en los huecos que en los electrones. Por lo tanto, Los agujeros permiten la manipulación de espín totalmente eléctrica, lo que es muy prometedor para transistores de espín de potencia ultrabaja, bits cuánticos de alta velocidad, y bits cuánticos topológicos tolerantes a fallos.
En el estudio, los investigadores demostraron un mecanismo completamente nuevo para controlar eléctricamente el giro de los agujeros en un pozo cuántico, explotando la inusual naturaleza de giro 3/2 de los agujeros. Gracias a la fuerte interacción espín-órbita, los investigadores demostraron que al utilizar únicamente campos eléctricos para aumentar el impulso de los agujeros, la división de Zeeman podría mejorarse hasta en un 300%.
La extrema capacidad de sintonización de la división de Zeeman a través de campos eléctricos abre nuevas posibilidades para futuros dispositivos basados en espines cuánticos, como transistores de espín, qubits de órbita giratoria, y puertas de lógica cuántica. También ayudará a realizar sistemas Majorana en sistemas superconductores de tipo p, permitiendo conducir el sistema a un régimen topológico bajo un campo magnético externo sin suprimir la superconductividad necesaria para soportar las excitaciones de Majorana.
Los investigadores también desarrollaron un nuevo método para extraer el factor g (cuantificación de la división de Zeeman) de las oscilaciones de magnetorresistencia de agujeros bidimensionales. mejorando los métodos convencionales que fallan para sistemas bidimensionales con una fuerte interacción espín-órbita.
Finalmente, la capacidad de controlar la interacción espín-órbita también es clave para desarrollar nuevos materiales topológicos, que actualmente se están investigando en FLEET por su potencial para proporcionar vías de resistencia ultrabaja para las corrientes eléctricas.
El estudio Electrical Control of the Zeeman Spin Splitting in Two-dimensional Hole Systems se publicó en Cartas de revisión física hoy dia, y fue seleccionado como sugerencia de los editores, presentado en Física .