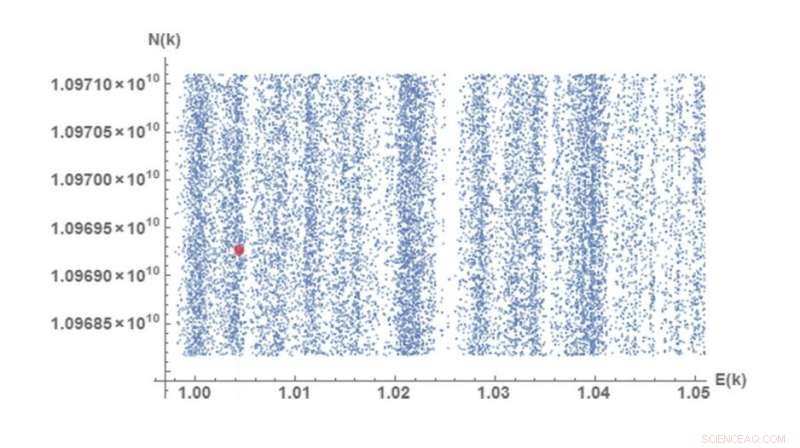
Esta gráfica de valores en el conjunto de factorización de 10, 000 muestra que los valores se correlacionan con el espectro de banda de un sistema cuántico. El punto rojo marca un ejemplo:el punto N =10, 969, 262, 131 =47, 297 x 231, 923, E =1,00441815 (donde Ek es una función descrita en el documento). Crédito:Rosales y Martín. © 2018 Sociedad Estadounidense de Física
Factorizar números muy grandes en sus "bloques de construcción" principales es extremadamente difícil para las computadoras clásicas, y esta dificultad subyace a la seguridad de muchos algoritmos criptográficos. Si bien es fácil factorizar el número 20 como el producto de los números primos 2 x 2 x 5, por ejemplo, factorizar números más grandes se vuelve exponencialmente más difícil cuando se utilizan algoritmos de factorización clásicos.
En un nuevo artículo publicado en Revisión física A , Los físicos José Luis Rosales y Vicente Martín han desarrollado un método que puede hacer mucho más fácil factorizar números muy grandes que se sabe que tienen exactamente dos factores primos. El nuevo método determina la probabilidad de que cualquier número primo sea uno de los dos factores primos de un número dado. Después de determinar estas probabilidades, los candidatos a factor primo más probables se pueden probar primero, permitiendo que los factores primos se identifiquen mucho más rápidamente que antes.
"La teoría muestra no solo dónde se encuentran los números primos, pero también la probabilidad de que un primo sea un factor de un número dado, "Rosales dijo Phys.org . "Por supuesto, esto tiene implicaciones en criptografía porque [el criptosistema] RSA ignora esta regularidad ".
Una de las cosas interesantes del nuevo método es que no utiliza ningún tipo de computadora, ya sea clásica o cuántica. En su lugar, implica un sistema cuántico físico, un "simulador cuántico", que, cuando se codifica con el número a factorizar, exhibe una distribución de probabilidad de valores de energía que es equivalente a la distribución de probabilidad de los factores primos candidatos del número codificado.
"Nuestro objetivo es desarrollar una nueva teoría cuántica del problema de factorización utilizando un simulador cuántico, ", Dijo Rosales." Nuestro enfoque ha descubierto una propiedad sin analogía clásica en la teoría de números. Cada par de números primos que resuelven el problema se reorganizan para formar un patrón regular:el espectro de bandas del simulador cuántico ".
La idea general detrás del simulador cuántico es algo llamado "conjunto de factorización, "que los investigadores introdujeron anteriormente. Se basa en la idea de que los números primos están ordenados de menor a mayor (por ejemplo, 2 es el primer primo, 3 es el segundo primo, y 101 es el 26 th principal). También es posible sacar la raíz cuadrada de cualquier número, y luego compare el resultado con el primo más cercano. Por ejemplo, la raíz cuadrada de 27 es un poco más de 5, que es el tercer primo. Según la definición de un conjunto de factorización, esto significa que 27 pertenece al conjunto de factorización de 3.
Los físicos demostraron entonces que podían transformar la función de conjunto de factorización en una función de la física cuántica (la función de oscilador armónico invertido). Después de muchos pasos más, finalmente demostraron que el espectro de energía predicho de un sistema cuántico corresponde a la distribución de números primos en el conjunto de factorización de un número. A partir de esta información, los investigadores pueden determinar la probabilidad de que un primo sea un factor de ese número. Para probar la validez de su método, los físicos probaron ciertos números y compararon sus resultados con las distribuciones reales obtenidas usando tablas de números primos, y encontró distribuciones muy similares.
Los físicos demostraron teóricamente que el simulador cuántico propuesto puede factorizar números que son muchos órdenes de magnitud más grandes que los que se han factorizado con las computadoras cuánticas. En su papel informan los resultados de usar su método para determinar la distribución de probabilidad de los factores primos de un número de 24 dígitos. Más lejos, el método hace esto con muchos menos recursos que los requeridos por los algoritmos de factorización clásicos.
"En teoría cuántica, la complejidad algorítmica es solo polinomial con el número de bits del número a factorizar, "Dijo Rosales." De hecho, nuestros primeros resultados parecen confirmar que el simulador solo requiere (log√N) 3 estados cuánticos para reproducir su espectro de energías, un resultado muy alentador ".
Un último punto de interés es que el nuevo método tiene fuertes conexiones con la hipótesis de Riemann, cuales, si es verdad, sugeriría que los números primos se distribuyen de una manera predecible, de la misma manera que la distribución de los ceros de la función de Riemann-zeta. Probar (o refutar) la hipótesis de Riemann es uno de los mayores problemas sin resolver en matemáticas, y uno de los Problemas del Premio Millennium del Clay Mathematics Institute.
"Los números primos deberían comportarse como números cuánticos si se aplica la conjetura de Hilbert-Polya, Rosales dijo, refiriéndose al enfoque de larga data para probar la hipótesis de Riemann.
Avanzando, los investigadores están trabajando actualmente en la implementación experimental del simulador cuántico utilizando dos partículas entrelazadas en una trampa de Penning.
"El tratamiento totalmente cuántico del simulador requeriría un análisis óptico cuántico de las interacciones de los fotones con dos (o más) iones entrelazados en una trampa de Penning, Rosales dijo. “Esta parte del programa aún está en desarrollo. El objetivo es construir experimentalmente un simulador de factorización cuántica. Si se implementa con éxito, Se factorizarán números muchos órdenes de magnitud mayores que los disponibles para su procesamiento cuántico utilizando el algoritmo de Shor y, como subproducto, la conjetura de Hilbert-Polya se probará experimentalmente ".
© 2018 Phys.org