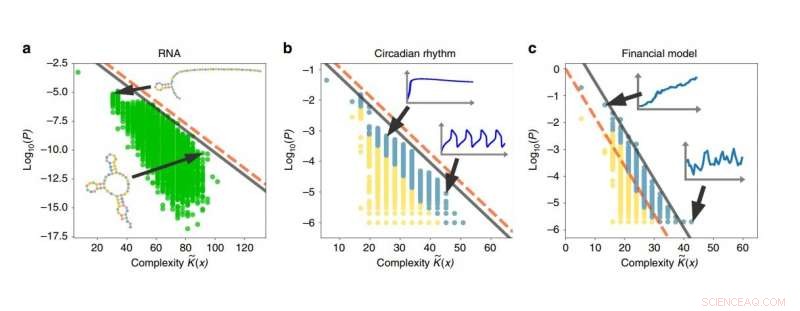
Ejemplos de sesgo de simplicidad en secuencias de ARN, ritmos circadianos, y modelos financieros. Cuanto mayor sea la complejidad de una salida, menor será la probabilidad de que se genere la salida. Crédito:Dingle, et al. Publicado en Comunicaciones de la naturaleza
Los investigadores han descubierto que los mapas de entrada-salida, que se utilizan ampliamente en la ciencia y la ingeniería para modelar sistemas que van desde la física hasta las finanzas, están fuertemente sesgados hacia la producción de resultados simples. Los resultados son sorprendentes, Tan ingenuamente, no hay razón para sospechar que un resultado debería ser más probable que cualquier otro.
Los investigadores, Kamaludin Dingle, Chico Q. Camargo, y Ard A. Louis, en la Universidad de Oxford y en la Universidad de Ciencia y Tecnología del Golfo, han publicado un artículo sobre sus resultados en un número reciente de Comunicaciones de la naturaleza .
"La mayor importancia de nuestro trabajo es nuestra predicción de que el sesgo de simplicidad (que es exponencialmente más probable que se generen salidas simples que salidas complejas) se aplica a una amplia variedad de sistemas en ciencia e ingeniería, "Louis dijo Phys.org . "El sesgo de simplicidad implica que, para un sistema formado por muchas partes diferentes que interactúan, digamos, un circuito con muchos componentes, una red con muchas reacciones químicas, etc., la mayoría de las combinaciones de parámetros y entradas deberían resultar en un comportamiento simple ".
El trabajo se basa en el campo de la teoría algorítmica de la información (AIT), que trata de las conexiones entre la informática y la teoría de la información. Un resultado importante de AIT es el teorema de codificación. Según este teorema, cuando una máquina de Turing universal (un dispositivo informático abstracto que puede calcular cualquier función) recibe una entrada aleatoria, Las salidas simples tienen una probabilidad exponencialmente mayor de generarse que las salidas complejas. Como explican los investigadores, este resultado está completamente en desacuerdo con la ingenua expectativa de que todos los resultados son igualmente probables.
A pesar de estos intrigantes hallazgos, Hasta ahora, el teorema de la codificación rara vez se ha aplicado a ningún sistema del mundo real. Esto se debe a que el teorema solo se ha formulado de una manera muy abstracta, y uno de sus componentes clave, una medida de complejidad llamada complejidad de Kolmogorov, es incontestable.
"El teorema de codificación de Solomonoff y Levin es un resultado notable que realmente debería ser mucho más conocido, "Dijo Louis." Predice que las salidas de baja complejidad son exponencialmente más propensas a ser generadas por una máquina de Turing universal (UTM) que las salidas de alta complejidad. Dado que cualquier cosa que sea computable se puede calcular en un UTM, ¡Esa es una predicción bastante sorprendente!
"Sin embargo, el teorema de codificación ha permanecido oscuro porque los UTM son bastante abstractos, porque solo se puede demostrar que se mantiene en el límite asintótico de las grandes complejidades, y porque la medida de Kolmogorov utilizada para determinar la complejidad es fundamentalmente incontestable. Nuestro trabajo evita estos problemas utilizando una versión ligeramente más débil del teorema de codificación que es mucho más fácil de aplicar ".
En el nuevo, versión más débil del teorema de codificación, los investigadores reemplazaron la complejidad de Kolmogorov con una complejidad de aproximación, que es computable, conservando al mismo tiempo la preferencia exponencial por la simplicidad. El teorema de codificación más débil se puede aplicar fácilmente para hacer predicciones sobre sistemas prácticos.
"Usamos el lenguaje de los mapas de entrada y salida, que puede sonar bastante abstracto, "Louis dijo." Sin embargo, muchos sistemas estudiados en ciencia e ingeniería convierten algún tipo de entrada en algún tipo de salida a través de un algoritmo. Por ejemplo, la información codificada en el ADN de un organismo (su genotipo) podría verse como entrada, mientras que las características y el comportamiento del organismo (su fenotipo) podrían verse como el resultado. En un conjunto de ecuaciones diferenciales, la entrada son los parámetros de las ecuaciones, y la salida es la solución de esas ecuaciones, dadas algunas condiciones de contorno.
"Argumentamos que si elige parámetros de entrada al azar, entonces, es exponencialmente más probable que estos sistemas produzcan salidas simples en lugar de salidas complejas. Dado que esta predicción es válida para una amplia gama de mapas, estamos haciendo una afirmación amplia. Pero ese es uno de sus puntos fuertes. Nuestra derivación no requiere saber mucho sobre cómo funciona realmente el mapa (o el algoritmo) en cuestión.
"Entonces, el significado principal de nuestro trabajo es que nuestra versión más débil del teorema de codificación mantiene aproximadamente el sesgo exponencial hacia la simplicidad del teorema de codificación original, pero es mucho más fácil de aplicar en la práctica ".
Una consecuencia de los resultados es que es posible predecir la probabilidad de cualquier resultado en particular en función de su complejidad. Aunque es exponencialmente más probable que aparezca una salida simple que una salida compleja, los investigadores señalan que esto no significa necesariamente que sea más probable que aparezcan salidas simples que salidas complejas en general, ya que puede haber muchos resultados más complejos que los simples en general.
Para ilustrar algunas aplicaciones, los investigadores utilizaron el teorema de codificación modificado para analizar sistemas de secuencias de ARN, ritmos circadianos, y mercados financieros, y mostró que todos estos sistemas exhiben el sesgo de simplicidad. En el futuro, también planean aplicar los resultados a algoritmos informáticos, evolución biológica, y sistemas caóticos. Sin embargo, para una explicación más intuitiva de lo que significa el sesgo de simplicidad, los investigadores describen un escenario que involucra a nuestros parientes primates:
"Considere el conocido problema de los monos escribiendo en una máquina de escribir, "Dijo Louis." Si los monos escriben de una manera verdaderamente aleatoria, y la maquina de escribir tiene norte teclas, entonces la probabilidad de obtener una secuencia particular de longitud k es solo 1 / norte k , ya que hay un 1 / norte posibilidad de obtener la pulsación de tecla correcta en cada uno de los k pasos. Así, cada secuencia de longitud k es igualmente probable o improbable.
"Ahora considere el caso en el que los monos están escribiendo en un programa de computadora. Es posible que, por accidente, escriban un programa corto que genere una salida larga. Por ejemplo, hay un código de 133 caracteres en el lenguaje de programación C que genera correctamente los primeros 15, 000 dígitos de π. Entonces en lugar de 1 / norte 15, 000 , cuál es la probabilidad de que los monos lo hagan bien en una máquina de escribir, las probabilidades son mucho menores, solo 1/ norte 133 , que los monos generan π en la computadora.
Resulta que la mayoría de los números no tienen programas cortos que los generen, así que lo mejor que pueden hacer los monos en la computadora con estos números es escribir un programa como 'imprimir número, ', lo cual es casi la probabilidad de que lo hicieran bien en una máquina de escribir de todos modos. Pero para salidas simples, la probabilidad es mucho mayor que para la máquina de escribir. Por definición, Las salidas simples se definen como aquellas que tienen programas cortos que las describen, y las salidas complejas son aquellas que solo pueden describirse mediante programas largos. Entonces π es, por definición, un número de baja complejidad, y, por lo tanto, es mucho más probable que lo generen monos que escriben en un programa de computadora que muchos otros números que no son simples.
"Lo que hace el teorema de codificación es convertir esta historia intuitiva en cuantitativa. Es más probable que los programas cortos se escriban al azar, y dado que las probabilidades de longitud k los programas también escalan como 1 / norte k , es exponencialmente mucho más probable que aparezcan salidas simples que complejas. Nuestra contribución es demostrar cómo calcular fácilmente la relación exponencial entre probabilidad y complejidad para muchos sistemas prácticos. Lo bueno es que no es necesario saber mucho sobre el mapa (o lo que es lo mismo, el algoritmo) para determinar si es probable que aparezca una salida o no. Para una buena primera aproximación, cuanto más comprimible es una salida, es más probable que aparezca en entradas aleatorias ".
© 2018 Phys.org