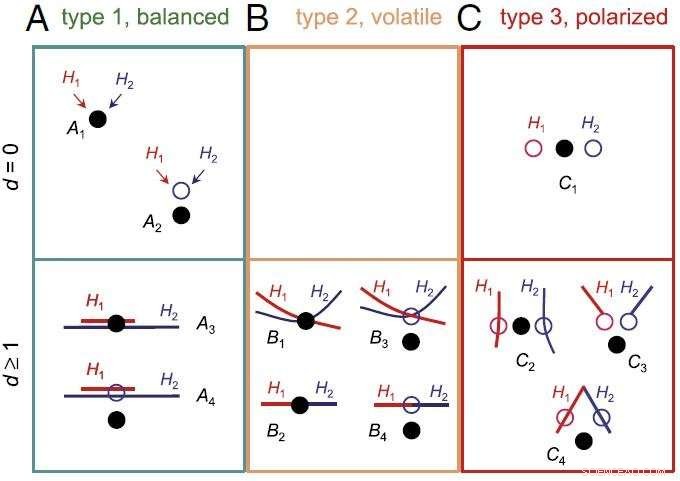
Clasificación de problemas de selección de modelos bayesianos que involucran dos modelos igualmente correctos o igualmente incorrectos. Crédito:ZHU Tianqi
Científicos del University College London (UCL) y la Academy of Mathematics and Systems Science, Academia China de Ciencias (CAS, AMSS), han informado avances en la comprensión de los problemas asociados con la selección del modelo bayesiano. La investigación sugiere que el método bayesiano tiende a producir probabilidades posteriores muy altas para árboles evolutivos estimados, incluso si los árboles están claramente equivocados. y ofrece una posible explicación de este fenómeno.
La comparación de modelos se usa ampliamente en varias ramas de las ciencias en las que las hipótesis científicas se formulan como modelos estadísticos y se prueban utilizando datos observados. Sin embargo, La comparación de modelos es un tema espinoso tanto en la estadística clásica como en la estadística bayesiana.
En estadística clásica, se comparan dos modelos anidados. El marco no funciona cuando los modelos comparados no están anidados. A diferencia de, La estadística bayesiana compara diferentes modelos calculando sus probabilidades posteriores, lo que indica nuestra confianza o creencia en el modelo.
Las dos metodologías no solo surgen de filosofías drásticamente diferentes, también pueden producir conclusiones opuestas en el análisis de los mismos datos. Se sabe que la selección del modelo bayesiano converge con el modelo verdadero si el modelo verdadero se incluye entre los modelos en consideración.
Es decir, cuando los científicos recopilan más datos, la probabilidad posterior para el modelo correcto aumentará y se acercará al 100 por ciento, y así estarán cada vez más seguros de cuál es el verdadero modelo.
Sin embargo, si todos los modelos considerados son incorrectos, se desconoce el comportamiento del método bayesiano.
Los científicos han caracterizado los problemas de selección del modelo bayesiano, y los categorizó en tres tipos, cada uno de los cuales muestra un comportamiento diferente.
En el caso más científicamente interesante, es decir., cuando los modelos comparados son distintos y casi igualmente incorrectos, La selección del modelo bayesiano muestra un comportamiento polarizado problemático:tiende a admitir un modelo con toda su fuerza en algunos conjuntos de datos, pero admite otro modelo en otros conjuntos de datos.
El resultado se puede resumir usando la siguiente analogía:Supongamos que el mundo es gris, pero le preguntamos a un sabio si es blanco o negro. Echa una mirada profunda al mundo y dice que es negro, con total confianza. Pero la próxima vez que hagamos la misma pregunta, dice que es blanco, de nuevo con total confianza.
Este estudio fue motivado por problemas en filogenética molecular, que es la ciencia de resolver las relaciones entre especies utilizando datos genéticos, representado por árboles evolutivos.
Estos diferentes árboles son modelos estadísticos opuestos en el análisis bayesiano de los datos. Los biólogos evolutivos han observado durante mucho tiempo que el método tiende a producir probabilidades posteriores muy altas para los árboles evolutivos estimados (muy a menudo el 100 por ciento), incluso si los árboles están claramente equivocados.
Nuestros resultados proporcionan una posible explicación de este comportamiento desagradable. Las implicaciones de los resultados para el uso de la selección del modelo bayesiano en la prueba de hipótesis científicas opuestas en general aún no se han explorado.