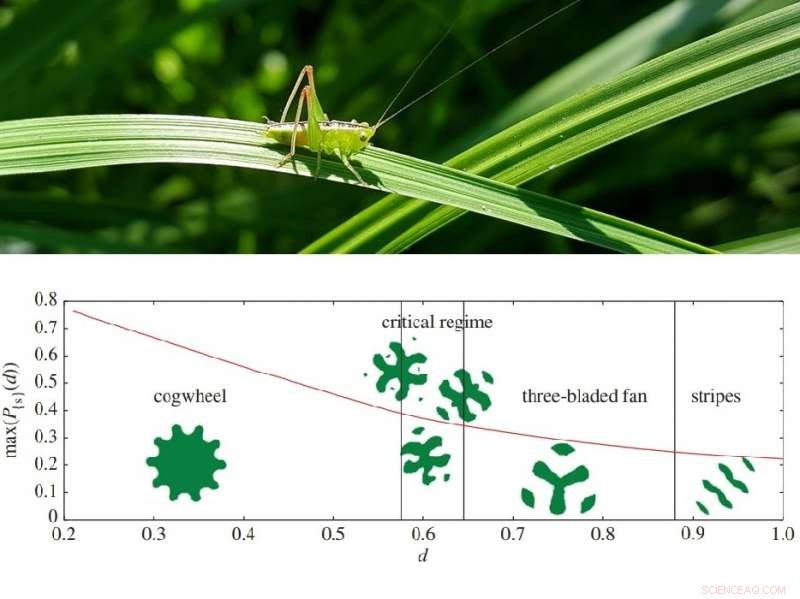
Algunas de las formas óptimas de césped, que dependen de la distancia que salte el saltamontes. Más allá del régimen crítico, las mejores configuraciones están desconectadas. Crédito del diagrama:Goulko et al. La Royal Society. Crédito:Pixabay.
(Phys.org):como muchos acertijos matemáticos, El problema del saltamontes es simple de enunciar pero difícil de resolver:un saltamontes aterriza en un punto aleatorio en un césped del área 1, luego salta una vez, una distancia fija, en una dirección aleatoria. ¿Qué forma debe tener el césped para maximizar la posibilidad de que el saltamontes se quede en el césped después de saltar?
Una primera impresión puede ser que el césped debe tener forma de círculo, al menos cuando la distancia que salta el saltamontes es pequeña. Sin embargo, Olga Goulko y Adrian Kent, los dos físicos que introdujeron el problema del saltamontes en un nuevo artículo, han demostrado matemáticamente que un césped en forma de disco no es óptimo para ninguna distancia.
En lugar de, descubrieron a través de simulaciones numéricas que la forma óptima del césped adquiere una variedad de formas complejas para diferentes distancias de salto, como una rueda dentada para distancias menores a 1 / π 1/2 (el radio de un círculo del área 1, o aproximadamente 0,56), mientras que para distancias mayores, el césped óptimo consiste en piezas desconectadas. A menudo, pero no siempre, estas formas óptimas poseen algún tipo de simetría.
Motivado por la física
Aparte de ser un problema de geometría interesante, El problema del saltamontes también está estrechamente relacionado con la investigación en física cuántica y puede tener una variedad de aplicaciones tecnológicas. En particular, el problema del saltamontes está relacionado con las desigualdades de Bell, que demuestran que, a diferencia de los modelos de física clásica, la teoría cuántica no obedece al realismo local. Un excelente ejemplo de la violación del realismo local se ve en el entrelazamiento cuántico, en el que dos sistemas entrelazados distantes exhiben correlaciones que no pueden ser explicadas por ningún modelo que obedezca al realismo local.
Esta conexión con las desigualdades de Bell es, De hecho, lo que motivó originalmente a Goulko y Kent a proponer el problema del saltamontes. Un problema abierto en física con respecto a las desigualdades de Bell es determinar los límites óptimos que viola la teoría cuántica cuando las correlaciones cuánticas se miden en una esfera en ángulos entre 0 y 90 grados. Resulta que este problema de determinar los límites óptimos es equivalente al problema de determinar la forma del césped del problema del saltamontes cuando el césped es esférico en lugar de terreno plano. En la versión esférica del problema del saltamontes, la distancia que el saltamontes salta sobre un terreno llano es reemplazada por el ángulo en el que salta a través de la esfera.
En su papel que se publica en un número reciente de la Actas de la Royal Society A , Goulko y Kent solo han analizado la versión plana del problema del saltamontes, aunque esperan que no sea demasiado difícil aplicar las mismas técnicas numéricas al caso esférico. Luego, al tener en cuenta algunas limitaciones adicionales, puede ser posible resolver finalmente el problema de los límites óptimos de las desigualdades de Bell.
"Planeamos avanzar para trabajar en las versiones esféricas del problema del saltamontes relevantes para las desigualdades de Bell, y esperamos que nuestros métodos funcionen allí, "Kent dijo Phys.org .
Nueva frontera
Como explican los físicos, Una de las cosas sorprendentes del problema del saltamontes es que nunca antes se había propuesto nada parecido. Aunque la idea básica es lo suficientemente sencilla como para que el problema pudiera haber sido planteado por el antiguo matemático griego Euclides, que sentó las bases de la geometría moderna, los investigadores no conocen ninguna versión anterior del problema, ya sea en tiempos antiguos o modernos.
"Es bueno recordar que, incluso en un campo tan antiguo como la geometría, todavía se pueden encontrar preguntas sencillas y novedosas que tienen respuestas sorprendentes y abren nuevas líneas de investigación, "Dijo Kent.
Como un problema completamente nuevo, Hay un sinfín de direcciones de investigación futuras a seguir. Por ejemplo, los físicos sugieren permitir que el saltamontes dé múltiples saltos, o exigir que el saltamontes camine y permanezca en el césped en todos los puntos de su camino (una variación que ellos llaman el "problema de las hormigas"). Otras posibles variaciones incluyen generalizar a dimensiones superiores, analizar superficies de césped distintas de esferas y planos, considerando una variación del problema con dos especies diferentes de semillas de césped que pueden superponerse en la misma región (lo cual es particularmente relevante para las desigualdades de Bell), y la imposición de restricciones adicionales a las posibles soluciones.
Por supuesto, estas preguntas no se refieren realmente a los saltamontes y el césped, ya que la estructura subyacente ofrece una forma de modelar varias situaciones del mundo real. Un ejemplo que señalan los investigadores son las reacciones nucleares en cadena. En una reacción en cadena, una partícula de alta energía impacta un núcleo atómico aleatorio, provocando que sufra fisión, que produce otra partícula de alta energía que viaja una cierta distancia para golpear otro núcleo aleatorio, y el proceso se repite. Al modelar esta situación con el problema del saltamontes, el área de césped óptima corresponde a la máxima velocidad de reacción inicial, lo que maximiza el número de núcleos que participan en la reacción en cadena.
Otra aplicación potencial del problema del saltamontes radica en el modelado de protocolos de comunicación cuántica, que los investigadores explican se puede considerar como un modelo de saltamontes en el que una de las partes debe elegir qué algoritmo (forma de césped) utilizar para comunicarse con una segunda parte.
Y finalmente, los investigadores sugieren que puede ser interesante investigar los orígenes de las propias formas del césped, ya que algunos de los patrones del césped se asemejan a patrones que surgen repetidamente en la naturaleza, como en flores, conchas marinas y rayas de animales. De acuerdo con la teoría de la morfogénesis propuesta por Alan Turing, estos patrones pueden surgir como soluciones óptimas por razones químicas, lo que puede ayudar a explicar las diversas y complejas formas del césped que aparecen en el problema del saltamontes.
© 2017 Phys.org