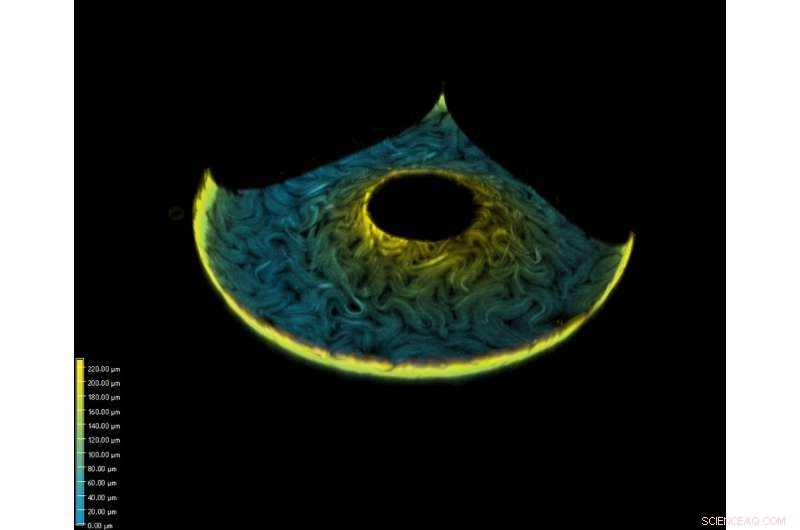
Imagen tomada de un toroide usando un microscopio confocal, falso coloreado por altura. Las estructuras parecidas a gusanos son microtúbulos impulsados por proteínas motoras kinesin. Crédito:Perry Ellis, Georgia Tech
Imagina una pequeña gota en forma de rosquilla, cubierto de gusanos que se retuercen. Los gusanos están tan juntos que deben alinearse localmente entre sí. En esta situación, diríamos que los gusanos forman un cristal líquido nemático, una fase ordenada similar a los materiales utilizados en muchas pantallas planas.
Sin embargo, la fase nemática formada por los gusanos está llena de pequeñas regiones donde se pierde la alineación local:defectos en el material alineado de otro modo. Además, porque los gusanos se mueven constantemente y cambian su configuración, esta fase nemática está activa y lejos del equilibrio.
En una investigación publicada en la revista Física de la naturaleza , Científicos del Instituto de Tecnología de Georgia y la Universidad de Leiden en los Países Bajos han descrito los resultados de un examen teórico y experimental combinado de un nemático tan activo en la superficie de gotitas toroidales en forma de rosquilla. Sin embargo, los investigadores no usaron gusanos reales, sino un nemático activo compuesto por filamentos flexibles cubiertos con motores microscópicos que constantemente convierten energía en movimiento.
Este material activo en particular, desarrollado originalmente en la Universidad de Brandeis, toma prestados elementos de la maquinaria celular, con haces de microtúbulos en forma de varillas que forman los filamentos, proteínas motoras de kinesina que actúan como motores, y ATP como combustible. Cuando esta actividad se combina con defectos, los defectos "cobran vida, "moverse como microorganismos nadadores y explorar el espacio, en este caso, explorando la superficie de las gotitas toroidales.
Al estudiar las gotas toroidales cubiertas por este nemático activo, los investigadores confirmaron una predicción teórica de larga data sobre los cristales líquidos en equilibrio, discutido por primera vez por Bowick, Nelson y Travesset [Phys.Rev. E 69, 041102 (2004)] que los defectos nemáticos en la superficie curva de tales gotas serán sensibles a la curvatura local. Sin embargo, dado que la nemática activa utilizada en este trabajo está lejos del equilibrio, los investigadores también encontraron cómo la actividad interna cambió y enriqueció las expectativas.
"Ha habido predicciones que dicen que los defectos son muy sensibles al espacio que habitan, específicamente a la curvatura del espacio, "dijo Perry Ellis, estudiante de posgrado en la Escuela de Física de Georgia Tech y primer autor del artículo. "El toro es un gran lugar para investigar esto porque el exterior del toro, la parte que localmente se ve como una esfera, tiene una curvatura positiva mientras que la parte interna de un toro, la parte que parece una silla de montar, tiene curvatura negativa ".
"La cantidad que caracteriza a un defecto es lo que llamamos su carga topológica o número de bobinado, "dijo Alberto Fernandez-Nieves, profesor de la Escuela de Física de Georgia Tech y otro de los coautores del artículo. "Expresa cómo cambia la dirección de alineación del cristal líquido nemático a medida que rodeamos el defecto. Esta carga topológica se cuantifica, lo que significa que solo puede tomar valores de un conjunto discreto que sean múltiplos de la mitad. "
En estos experimentos, cada defecto tiene una carga topológica de +1/2 o -1/2. Para determinar la carga y la ubicación de cada defecto, Ellis observó las gotas toroidales a lo largo del tiempo usando un microscopio confocal y luego analizó el video resultante usando técnicas tomadas de la visión por computadora. Los investigadores encontraron que incluso con los motores moleculares que conducen al sistema fuera de equilibrio, los defectos aún podían sentir la curvatura, con los defectos +1/2 migrando hacia la región de curvatura positiva y los defectos -1/2 migrando hacia la región de curvatura negativa.
En este nuevo trabajo, los científicos dieron un paso adelante en la comprensión de cómo controlar y guiar los defectos en un material ordenado.
"Hemos aprendido que podemos controlar y guiar la materia activa parcialmente ordenada utilizando la curvatura del sustrato subyacente, ", dijo Fernández-Nieves." Este trabajo abre oportunidades para estudiar cómo los defectos en estos materiales se colocan en superficies que no tienen una curvatura constante. Esto abre la puerta para controlar la materia activa mediante la curvatura ".
Un hallazgo inesperado del estudio fue que el movimiento constante de los defectos hace que la carga topológica promedio se vuelva continua, ya no se toman solo valores que son múltiplos de la mitad.
"En el límite activo de nuestros experimentos, encontramos que la carga topológica se convierte en una variable continua que ahora puede tomar cualquier valor, ", dijo Fernández-Nieves." Esto recuerda lo que sucede con muchos sistemas cuánticos a alta temperatura, donde el cuanto, Se pierde la naturaleza discreta de los estados accesibles y las variables asociadas.
En lugar de caracterizarse por propiedades cuantificadas, el sistema se caracteriza por propiedades continuas ".
Las observaciones de Ellis de las gotas se compararon bien con las de las simulaciones numéricas realizadas por el profesor asistente Luca Giomi y el investigador postdoctoral Daniel Pearce en el Instituut-Lorentz de Física Teórica de la Universiteit Leiden en los Países Bajos.
"Nuestro modelo teórico nos ayudó a descifrar los resultados experimentales y comprender completamente el mecanismo físico que gobierna el movimiento del defecto, "dijo Pearce, "pero también nos permitió ir más allá de la evidencia experimental actual". Giomi agregó:"La actividad cambia la naturaleza de la interacción entre los defectos y la curvatura. En sistemas débilmente activos, los defectos son atraídos por regiones de curvatura gaussiana de signo similar. Pero en sistemas fuertemente activos, este efecto se vuelve menos relevante y los defectos se comportan como persistentes caminantes aleatorios confinados en un espacio cerrado y no homogéneo ”.
Hay muchos ejemplos de sistemas activos impulsados por la actividad interna, incluidos los microorganismos natadores, bandadas de aves, enjambres de robots y flujos de tráfico. "Los materiales activos están en todas partes, por lo que nuestros resultados no se limitan solo a este sistema en un toro, "Ellis agregó." Se puede ver el mismo comportamiento en cualquier sistema activo con defectos ".
La investigación sienta las bases para el trabajo futuro en fluidos activos. "Nuestros resultados introducen un nuevo marco para explorar las propiedades mecánicas de los fluidos activos y sugieren que la materia activa parcialmente ordenada se puede guiar y controlar a través de gradientes en la geometría intrínseca del sustrato subyacente". "escribieron los autores en un resumen de su artículo.