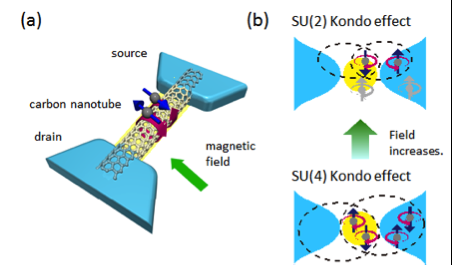
Figura 1:(a) Los grados de libertad de giro y orbital de los electrones en un punto cuántico de nanotubos de carbono se muestran mediante las flechas azules rectas y las flechas de círculo púrpura, respectivamente. Podemos controlar el número de electrones en el punto cuántico uno por uno mediante el electrodo de puerta cercano (no se muestra en la figura). (b) Debido a los grados de libertad de giro y orbital, Se forma un estado SU (4) Kondo con un campo magnético cero, como se muestra en el panel inferior. En un campo magnético alto, evoluciona continuamente a un efecto Kondo SU (2) (panel superior). Crédito:Universidad de Osaka
Las transiciones de fase incluyen fenómenos comunes como congelación o ebullición del agua. Similar, Los sistemas cuánticos a una temperatura de cero absoluto también experimentan transiciones de fase. La presión o el campo magnético aplicado a tales sistemas se puede ajustar para que estos sistemas lleguen a un punto de inflexión entre dos fases. En este punto las fluctuaciones cuánticas, en lugar de fluctuaciones de temperatura, impulsar estas transiciones.
Muchos fenómenos fascinantes con aplicaciones tecnológicas prometedoras en áreas como la superconductividad están relacionados con las transiciones de fase cuántica, pero el papel de las fluctuaciones cuánticas en tales transiciones sigue sin estar claro. Si bien ha habido muchos avances en la comprensión del comportamiento de partículas individuales como los protones, neutrones, y fotones, El desafío de comprender los sistemas que contienen muchas partículas que interactúan fuertemente entre sí aún no se ha resuelto.
Ahora, un equipo de investigación internacional dirigido por un grupo de la Universidad de Osaka ha descubierto un vínculo claro entre las fluctuaciones cuánticas y la carga efectiva de las partículas portadoras de corriente. Este descubrimiento ayudará a los investigadores a descubrir cómo las fluctuaciones cuánticas gobiernan los sistemas en los que interactúan muchas partículas. Un ejemplo de tal sistema es la interacción de electrones a temperaturas extremadamente bajas. Si bien las bajas temperaturas normalmente hacen que disminuya la resistencia de un metal, la resistencia aumenta de nuevo a temperaturas extremadamente bajas debido a pequeñas impurezas magnéticas; esto se conoce como efecto Kondo.
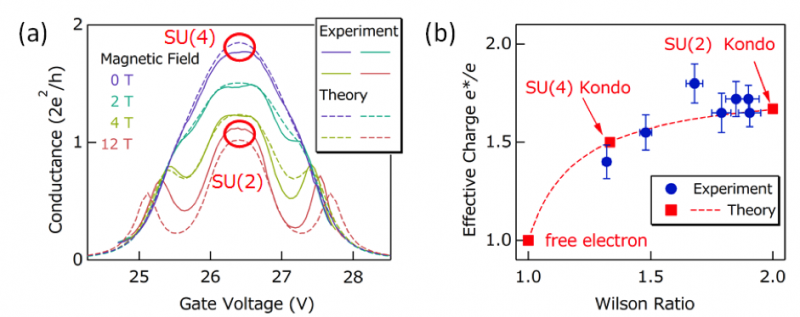
Figura 2:(a) Conductancia del punto cuántico en función del voltaje de la puerta. La conductancia está normalizada por el cuanto de conductancia (2e2 / h). Los datos experimentales (líneas continuas) y los resultados de los cálculos del grupo de renormalización numérica (NRG) (líneas discontinuas) son cuantitativamente coherentes entre sí. (b) Los círculos llenos muestran la carga efectiva e * / e en función de la relación de Wilson que cuantifica la fuerza de las fluctuaciones. La carga efectiva e * / e se deriva del ruido actual y la relación de Wilson representa fluctuaciones cuánticas. Tres símbolos cuadrados representan la predicción teórica para SU (4), SU (2), y partículas que no interactúan. La línea discontinua es la predicción teórica extendida, que conecta muy bien el cruce de simetría de los estados básicos del líquido cuántico. Crédito:Universidad de Osaka
"Usamos un campo magnético para sintonizar el estado de Kondo en un nanotubo de carbono, asegurando que las fluctuaciones cuánticas fueran la única variable en el sistema, ", dice el coautor del estudio Kensuke Kobayashi." Al monitorear directamente la conductancia y el ruido de disparo del nanotubo de carbono, pudimos demostrar un cruce continuo entre los estados de Kondo con diferentes simetrías ".
Usando este enfoque novedoso, los investigadores descubrieron un vínculo entre las fluctuaciones cuánticas y la carga efectiva de las partículas portadoras de corriente, mi*. El descubrimiento significa que las mediciones de e * se pueden utilizar para cuantificar las fluctuaciones cuánticas.
"Esto es muy emocionante, ya que allana el camino para futuras investigaciones sobre el papel exacto de las fluctuaciones cuánticas en las transiciones de fase cuántica, "explica el profesor Kobayashi. Comprender las transiciones de fase cuántica tiene el potencial de permitir muchas aplicaciones interesantes en áreas como la superconductividad, Aisladores Mott, y el efecto Hall cuántico fraccional.