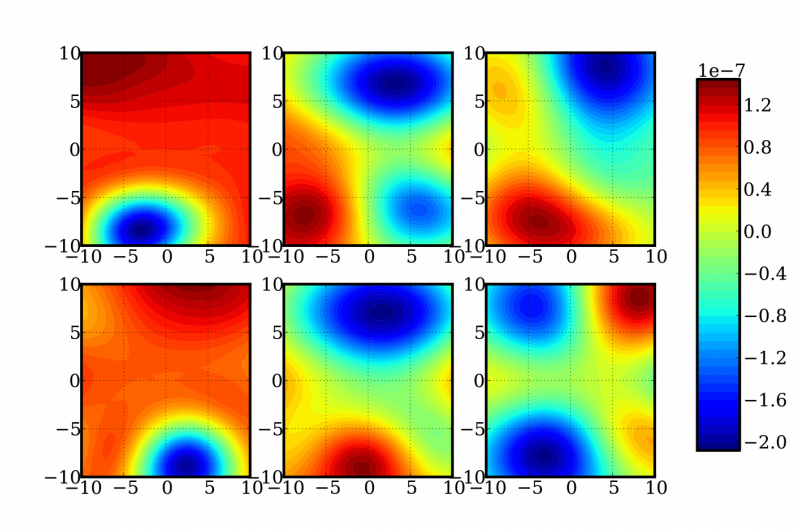
Representación de cortes bidimensionales aleatorios de una función de 12 dimensiones para determinar las correcciones de energía y frecuencia de una molécula de formaldehído. Crédito:Laboratorios Nacionales Sandia
Los investigadores de Sandia National Laboratories han desarrollado nuevas técnicas matemáticas para avanzar en el estudio de moléculas a nivel cuántico.
Los desarrollos matemáticos y algorítmicos en esta línea son necesarios para permitir el estudio detallado de moléculas complejas de hidrocarburos que son relevantes en la combustión de motores.
Los métodos existentes para aproximar las funciones de energía potencial a escala cuántica necesitan demasiada potencia de computadora y, por lo tanto, se limitan a moléculas pequeñas. Los investigadores de Sandia dicen que su técnica acelerará los cálculos de la mecánica cuántica y mejorará las predicciones realizadas por los modelos químicos teóricos. Dada la aceleración computacional, estos métodos pueden potencialmente aplicarse a moléculas más grandes.
El investigador postdoctoral de Sandia, Prashant Rai, trabajó con los investigadores Khachik Sargsyan y Habib Najm en las instalaciones de investigación de combustión de Sandia y colaboró con los químicos cuánticos So Hirata y Matthew Hermes en la Universidad de Illinois en Urbana-Champaign. Calcular la energía con menos disposiciones geométricas de las que se requieren normalmente, el equipo desarrolló métodos computacionalmente eficientes para aproximar superficies de energía potencial.
Una comprensión precisa de las superficies de energía potencial, elementos clave en prácticamente todos los cálculos de dinámica cuántica, es necesario para estimar con precisión la energía y la frecuencia de los modos vibratorios de las moléculas.
"Si podemos encontrar la energía de la molécula para todas las configuraciones posibles, podemos determinar información importante, como estados estables de estructura de transición molecular o estados intermedios de moléculas en reacciones químicas, "Dijo Rai.
Los resultados iniciales de esta investigación se publicaron en Física molecular en un artículo titulado "Descomposición de tensor canónico de bajo rango de superficies de energía potencial:aplicación a la teoría de función de Green vibracional esquemática basada en cuadrículas".

Los investigadores de Sandia National Laboratories Prashant Rai, izquierda, Habib Najm, centrar, y Khachik Sargsyan discuten las técnicas matemáticas utilizadas para estudiar el comportamiento de moléculas grandes a escala cuántica. Crédito:Dino Vournas
"Aproximar las superficies de energía potencial de moléculas más grandes es una tarea extremadamente desafiante debido al aumento exponencial de la información requerida para describirlas con cada átomo adicional en el sistema". "Rai dijo." En matemáticas, se denomina la maldición de la dimensionalidad ".
Venciendo la maldición
La clave para vencer la maldición de la dimensionalidad es explotar las características de la estructura específica de las superficies de energía potencial. Rai dijo que esta información de estructura se puede usar para aproximar las funciones de alta dimensión requeridas.
"Aprovechamos el hecho de que, aunque las superficies de energía potencial pueden ser de gran dimensión, pueden aproximarse bien como una pequeña suma de productos de funciones unidimensionales. Esto se conoce como estructura de rango bajo, donde el rango de la superficie de energía potencial es el número de términos en la suma, "Dijo Rai." Tal suposición sobre la estructura es bastante general y también se ha utilizado en problemas similares en otros campos. Matemáticamente, la intuición de las técnicas de aproximación de bajo rango proviene del álgebra multilineal donde la función se interpreta como un tensor y se descompone usando técnicas estándar de descomposición de tensor ".
Las correcciones de energía y frecuencia se formulan como integrales de estas funciones de energía de alta dimensión. La aproximación en un formato de rango tan bajo hace que estas funciones sean fácilmente integrables, ya que rompe el problema de integración con la suma de productos de integrales unidimensionales o bidimensionales. por lo que se aplican los métodos de integración estándar.
El equipo probó sus métodos computacionales en moléculas pequeñas como agua y formaldehído. En comparación con el método clásico de Monte Carlo, el caballo de batalla estándar basado en la aleatoriedad para problemas de integración de alta dimensión, su enfoque predijo la energía y la frecuencia de la molécula de agua que eran más precisas, y fue al menos 1, 000 veces más eficiente computacionalmente.
Rai dijo que el siguiente paso es mejorar aún más la técnica desafiándola con moléculas más grandes, como el benceno.
"Estudios Interdisciplinarios, como la química cuántica y la ingeniería de combustión, Brindar oportunidades para la polinización cruzada de ideas. proporcionando así una nueva perspectiva sobre los problemas y sus posibles soluciones, ", Dijo Rai." También es un paso hacia el uso de los avances recientes en la ciencia de datos como un pilar del descubrimiento científico en el futuro ".