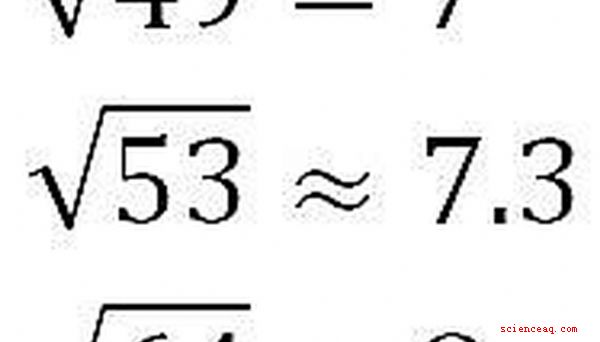
En matemáticas, a veces es importante para nosotros poder estimar los valores de las raíces cuadradas (radicales). Este es especialmente el caso de los exámenes que no permiten el uso de una calculadora, y está tratando de eliminar las respuestas incorrectas, o verificar la razonabilidad de su respuesta. Además, en geometría, los valores sqrt (2) y sqrt (3) aparecen con tanta frecuencia que es esencial conocer sus valores aproximados.
Este artículo muestra los pasos para estimar una raíz cuadrada. El artículo supone que tienes una comprensión básica de las raíces cuadradas y los cuadrados perfectos. Vea la sección de Referencia para más información.
Para estimar el valor de la raíz cuadrada de un número, encuentre que los cuadrados perfectos están arriba y abajo del número. Por ejemplo, para estimar sqrt (6), observe que 6 está entre los cuadrados perfectos 4 y 9. Sqrt (4) = 2, y sqrt (9) = 3. Dado que 6 está más cerca de 4 que de 9, esperaría que su raíz cuadrada esté más cerca de 2 que 3. Es en realidad aproximadamente 2.4, pero mientras usted supiera que estaba en ese estadio, estaría bien. Incluso el simple hecho de saber que estaba entre 2 y 3 sería una ventaja para usted.
Probemos otro ejemplo. Estimar sqrt (53). 53 está entre los cuadrados perfectos 49 y 64, cuyas raíces cuadradas son 7 y 8, respectivamente. 53 está más cerca de 49 que de 64, por lo que sería razonable estimar que sqrt (53) esté entre 7 y 7.5. Resulta que es aproximadamente 7.3.
Hay dos raíces cuadradas que surgen con mucha frecuencia en geometría. Son sqrt (2) y sqrt (3). Es muy importante que memorices sus valores aproximados. Tenga en cuenta que sqrt (1) es 1 y sqrt (4) es 2. En base a esto, no debe sorprender que sqrt (2) sea aproximadamente 1.4, y sqrt (3) es aproximadamente 1.7.
Lo más importante es recordar que sqrt (2) es mayor que 1, y sqrt (3) es menor que 2. Otro artículo discute la aplicación de estas raíces cuadradas al trabajar con triángulos rectos y el Teorema de Pitágoras.
Los estudiantes deben asegurarse de que se sienten cómodos con la estimación de las raíces cuadradas, y para el caso, estimar todas sus respuestas para ver si son razonables. Esto generalmente le permitirá detectar sus errores antes de entregar sus exámenes.