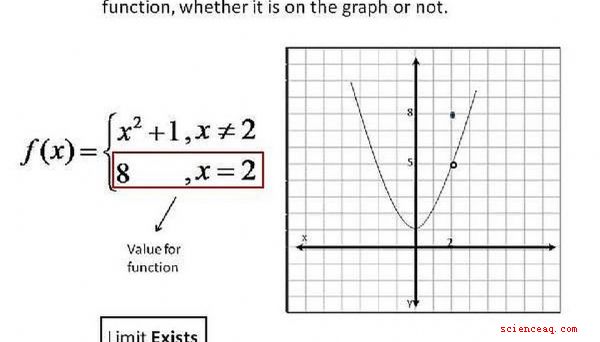
Vamos a usar algunos ejemplos de funciones y sus gráficos para mostrar cómo podemos determinar si el límite existe cuando x se acerca a un número en particular.

Hay cuatro formas diferentes de determinar si existe un límite por mirando el gráfico para la función. El primero, que muestra que el límite sí existe, es si el gráfico tiene un agujero en la línea, con un punto para ese valor de x en un valor diferente de y. Si esto sucede, entonces el límite existe, aunque tiene un valor diferente para la función que el valor para el límite. Haga clic en la imagen para una mejor comprensión.

Si hay un agujero en el gráfico en el valor que x se acerca, sin otro punto para un valor diferente de la función, entonces el límite todavía existe . Consulte el gráfico para una mejor comprensión.

Si el gráfico tiene una asíntota vertical, es decir, dos líneas que se aproximan al valor del límite que continúa hacia arriba o hacia abajo sin límites, entonces el límite no existe. Haga clic en la imagen para una mejor comprensión.

Si el gráfico se acerca a dos números diferentes desde dos direcciones diferentes, cuando x se acerca a un número en particular, entonces el límite no existe. No pueden ser dos números diferentes. Haga clic en la imagen para una mejor comprensión.