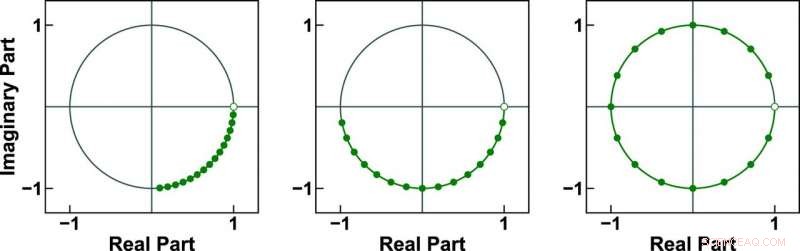
Aquí hay tres ejemplos de contornos de chirrido de 16 puntos en el círculo unitario. El algoritmo ICZT desarrollado por los ingenieros del estado de Iowa puede funcionar con los tres, mientras que el que se utilizó anteriormente solo puede funcionar con el último contorno. Crédito:Alexander Stoytchev.
Alexander Stoytchev, de la Universidad Estatal de Iowa, dice que es uno de los algoritmos "más populares y útiles" que existen, aunque la mayoría de nosotros nunca ha oído hablar de él.
Pero, si has usado un celular, navegó por Internet o necesitaba una imagen médica, se ha beneficiado de la transformada rápida de Fourier (FFT).
La transformación y su inversa (conocida como IFFT) se han utilizado desde 1965. Por ejemplo, en su teléfono celular, la FFT se usa para analizar la señal recibida desde la estación base (o torre celular). El IFFT resuelve el problema inverso:sintetiza la señal que su teléfono envía a la estación base.
En 1969, los investigadores desarrollaron un método más útil, versión generalizada de la FFT conocida como transformación z de chirp (CZT). Pero a nadie se le había ocurrido una versión generalizada del IFFT. Era un rompecabezas de 50 años en el procesamiento de señales.
Es decir, hasta el otoño pasado, cuando dos ingenieros del estado de Iowa, Stoytchev y Vladimir Sukhoy, anunciaron en un artículo de investigación que habían creado una solución de forma cerrada para la transformada z de chirp inverso (ICZT) y un algoritmo rápido para calcularla. (El artículo despertó mucho interés en la comunidad de procesamiento de señales, sumando más de 26, 000 accesos desde octubre.)
Ahora Stoytchev, profesor asociado de ingeniería eléctrica e informática que también está afiliado al Centro de Aplicaciones de Realidad Virtual de la universidad, y Sukhoy, profesor de ingeniería eléctrica e informática, informan sobre nuevos resultados de investigación sobre su algoritmo.
En un artículo recién publicado en línea por Informes científicos , una revista Nature Research, los dos muestran cómo funciona su algoritmo "en el círculo unitario, "que se refiere a un caso especial de sus parámetros. (Su artículo anterior solo resaltaba las operaciones" fuera del círculo unitario ").
El documento detalla cómo el algoritmo puede funcionar con componentes de frecuencia que son generados por puntos de muestra del círculo unitario en el plano complejo. Estos puntos forman un contorno que se conoce como contorno de chirrido. A diferencia de IFFT, que solo puede funcionar con puntos de muestreo equiespaciados que cubren completamente el círculo unitario, el algoritmo ICZT puede trabajar con contornos que cubren solo una fracción del círculo unitario. También puede trabajar con contornos que envuelven y realizan múltiples revoluciones sobre el círculo. Esto permite el uso de ciertos componentes de frecuencia (no ortogonales), lo que elimina una de las principales restricciones de la IFFT y podría conducir a una mejor utilización del espectro.
El documento identifica los valores de los parámetros para los que el algoritmo es numéricamente preciso y para los que no lo es. y describe cómo estimar su precisión en función de los parámetros. (Nota técnica:muestra que las singularidades del ICZT de tamaño n están relacionadas con los elementos de la secuencia de Farey de orden n-1. Esta es una conexión interesante porque las secuencias de Farey a menudo aparecen en la teoría de números).
El documento demuestra que, en el círculo unitario, el algoritmo ICZT logra una alta precisión con solo números de punto flotante de 64 bits y no requiere precisión numérica adicional, facilitando su implementación. Informa que el algoritmo puede emparejarse bien con el algoritmo CZT existente para realizar análisis y síntesis de señales consecutivos. Y muestra que el algoritmo es rápido (opera en lo que se conoce como tiempo O (n log n)).
"Este algoritmo es más general que el IFFT, pero mantiene la misma velocidad, "Dijo Stoytchev.
Esas son buenas noticias para los ingenieros que trabajan para resolver todo tipo de desafíos de procesamiento de señales:
"Dominios de aplicaciones que podrían beneficiarse de esto, "escribieron los ingenieros del estado de Iowa en el periódico, "incluyen procesamiento de señales, electrónica, imagenes medicas, Radar, sonar, comunicaciones inalámbricas, y otros."