Un estudio publicado en la revista Physical Review Letters por investigadores en Japón resuelve un problema de larga data en la física cuántica al redefinir el principio de incertidumbre.
El principio de incertidumbre de Werner Heisenberg es una característica clave y sorprendente de la mecánica cuántica, y puede agradecerle a su fiebre del heno por ello. Miserable en Berlín en el verano de 1925, el joven físico alemán pasó sus vacaciones en la remota y rocosa isla de Helgoland, en el Mar del Norte, frente a la costa norte de Alemania. Sus alergias mejoraron y pudo continuar su trabajo tratando de comprender las complejidades del modelo atómico de Bohr, desarrollando tablas de propiedades atómicas internas, como energía, posición y momento.
Cuando regresó a Göttingen, su asesor, Max Born, reconoció que cada una de estas tablas podía formar una matriz, esencialmente una tabla de valores bidimensional. Junto con Pasqual Jordan, de 22 años, perfeccionaron su trabajo en la mecánica matricial, la primera teoría exitosa de la mecánica cuántica, las leyes físicas que describen objetos diminutos como átomos y electrones.
Si bien la mecánica matricial sería reemplazada en unos años por la función de onda de Schrödinger y su ecuación, le permitió a Heisenberg la idea de formular el principio de incertidumbre:hay un límite en la precisión con la que se pueden determinar la ubicación y el momento de un sistema cuántico, típicamente una partícula. medido.
El límite del producto de las incertidumbres de medición de las dos cantidades es h/4π, donde h es la constante de Planck, extremadamente pequeña pero no nula. En resumen, no se puede medir tanto la posición como el impulso de un objeto cuántico con una precisión arbitraria; medir uno con mayor precisión significa que el otro solo puede medirse con una precisión menor.
Desde un punto de vista físico, supongamos que queremos medir la posición y el momento de un electrón. Es necesario iluminar algún tipo de luz sobre un sistema para poder medir sus propiedades. La luz se cuantifica en forma de fotones, que tienen una energía distinta de cero. Hacer brillar un fotón sobre el electrón necesariamente lo perturba de su estado original. En mecánica cuántica el mero acto de medir impone un límite a la precisión de la medición.
Incertidumbres similares se aplican a las mediciones de tiempo y energía, posición angular y momento angular y, en general, a dos variables cualesquiera que no "conmutan" cuando se representan como operadores en una mecánica cuántica rigurosa.
Unas décadas más tarde, los físicos Eugene Wigner, luego Huzihiro Araki y Mutsuo M. Yanase refinaron el principio de incertidumbre en el teorema de Wigner-Araki-Yanase (WAY), que establece que para dos cantidades observables q y p, donde p se conserva ( como el momento de un sistema), incluso si p no se mide en absoluto, q no se puede medir con precisión arbitraria.
"Como consecuencia del teorema WAY podemos ver que (en cierto sentido) es imposible medir la posición de la partícula q; lo único que podemos medir es su posición relativa al aparato, q—Q", dijo el matemático John Baez de la La Universidad de California en Riverside ha escrito, donde Q es la posición del aparato de medición.
Pero el teorema WAY solo se aplica a cantidades como el espín de una partícula, que solo puede aceptar cantidades discretas y acotadas.
Ahora Yui Kuramochi de la Universidad de Kyushu y Hiroyasu Tajima de la Universidad de Electrocomunicaciones de Japón han resuelto un problema de larga data al demostrar que el teorema WAY también se aplica a cantidades observables que son continuas (no discretas) o ilimitadas, como la posición.
"Según el principio de incertidumbre, la posición y el impulso no pueden medirse con precisión simultáneamente", afirmó Kuramochi. "Nuestro resultado presenta una restricción adicional:ni siquiera la posición misma puede medirse con precisión, siempre y cuando utilicemos medidas naturales que satisfagan la conservación del impulso". Su prueba examina un "operador ilimitado", cantidades físicas que pueden tomar valores infinitamente grandes.
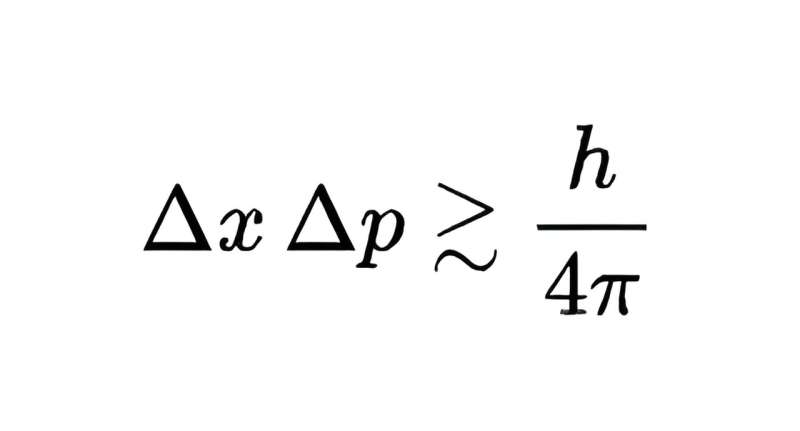
Estrictamente hablando, el resultado requiere una condición particular que subyace al teorema WAY, llamada condición de Yanase. Si bien es muy técnico, esencialmente estipula la compatibilidad de la variable ilimitada del aparato con la cantidad conservada. La condición de Yanase, aunque matemática, parece deseada por las aplicaciones a sistemas físicos del mundo real.
"El teorema WAY predice que, según una ley de conservación, una cantidad física que no conmuta con la carga conservada no puede medirse sin error", continúa Kuramochi. "Esto corresponde a una respuesta a un problema abierto desde hace 60 años. El nuevo resultado resuelve un problema de décadas de cómo abordar observables tan continuos e ilimitados, especialmente en campos como la óptica cuántica, donde es probable que la nueva extensión del teorema encuentre aplicaciones. ."
El teorema WAY original prohíbe que el error de medición sea cero, pero es un teorema cualitativo y no especifica el límite de medición ni siquiera si existe un límite inferior mayor que cero. Lo mismo se aplica a esta extensión del teorema WAY de Kuramochi y Tajima.
En su artículo, los autores escriben que todavía es una cuestión abierta si el teorema WAY original para mediciones repetidas puede generalizarse como lo han hecho, a observables conservados ilimitados.
Al sugerir nuevas direcciones de investigación sobre las extensiones del teorema WAY, al equipo le gustaría generalizar sus resultados a estados con restricción de energía, ya que sus resultados actuales están restringidos a casos independientes del estado y a casos aproximados. Una aplicación potencial es establecer límites sobre cómo los protocolos de transmisión de redes cuánticas pueden funcionar mejor que los límites clásicos.
Más información: Yui Kuramochi et al, Teorema de Wigner-Araki-Yanase para observables conservados continuos e ilimitados, Cartas de revisión física (2023). DOI:10.1103/PhysRevLett.131.210201
Información de la revista: Cartas de revisión física
© 2023 Red Ciencia X