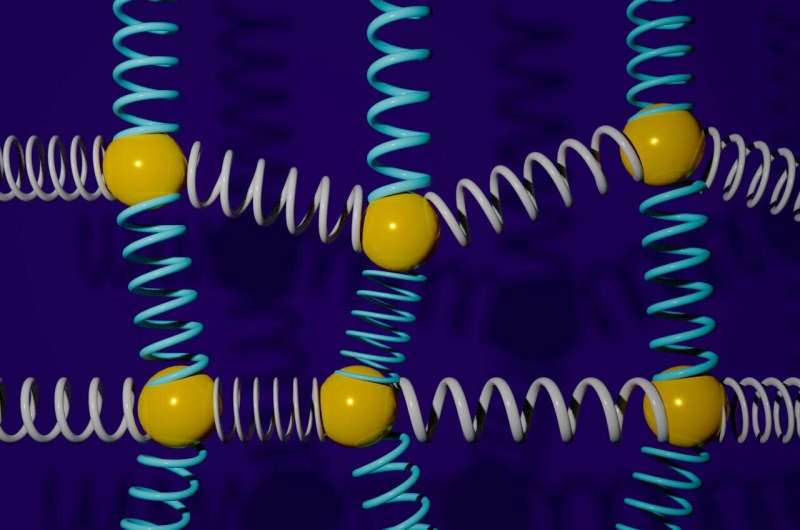
Aunque las "oscilaciones acopladas" pueden no parecer familiares, están en todas partes de la naturaleza. El término "osciladores armónicos acoplados" describe sistemas de masas y resortes que interactúan, pero su utilidad en la ciencia y la ingeniería no termina ahí. Describen sistemas mecánicos como puentes, enlaces entre átomos e incluso efectos de marea gravitacionales entre la Tierra y la Luna. Comprender estos problemas nos permite probar una gama correspondientemente amplia de sistemas, desde la química hasta la ingeniería, la ciencia de los materiales y más.
Representados clásicamente por un modelo de bola y resorte, los sistemas oscilatorios acoplados se vuelven cada vez más complejos a medida que se agregan más osciladores. Con un nuevo algoritmo cuántico creado en parte por el profesor Nathan Wiebe, designado conjuntamente por el Laboratorio Nacional del Noroeste del Pacífico (PNNL) y el profesor de la Universidad de Toronto, la simulación de sistemas de osciladores acoplados tan complejos es ahora más rápida y eficiente. Estos resultados fueron publicados en Physical Review X .
En asociación con investigadores de Google Quantum AI y la Universidad Macquarie en Sydney, Australia, Wiebe desarrolló un algoritmo para simular sistemas de masas y resortes acoplados en computadoras cuánticas. Luego, los investigadores proporcionaron evidencia de la ventaja exponencial del nuevo algoritmo sobre los algoritmos clásicos.
Esta aceleración fue posible mapeando la dinámica de los osciladores acoplados a una ecuación de Schrödinger, la contraparte cuántica de una ecuación newtoniana clásica. A partir de ahí, el sistema podría simularse utilizando métodos hamiltonianos.
En esencia, este enfoque permite a los científicos expresar la dinámica de osciladores acoplados utilizando muchos menos bits cuánticos que los métodos tradicionales. Luego, los investigadores pueden simular el sistema utilizando exponencialmente menos operaciones.
Quizás el aspecto más intrigante de su trabajo surge de la cuestión de si este algoritmo ofrece realmente una aceleración exponencial sobre todos los algoritmos ordinarios posibles. Primero, los autores demostraron que este algoritmo funciona en ambos sentidos:que los osciladores armónicos acoplados pueden usarse para simular una computadora cuántica arbitraria.
Esto significa que, a un alto nivel, sistemas muy grandes de masas y resortes que interactúan pueden contener en su interior una potencia computacional equivalente a la de una computadora cuántica.
En segundo lugar, los autores consideraron las limitaciones teóricas en torno al cálculo de estas dinámicas. Si existiera una manera de simular esta dinámica en tiempo polinómico en las computadoras existentes, entonces los investigadores podrían construir un método más rápido para simular computadoras cuánticas. Sin embargo, esto demostraría que los ordenadores cuánticos no son esencialmente más potentes que los ordenadores clásicos.
La evidencia acumulada a lo largo de los años muestra que es excepcionalmente improbable que las computadoras clásicas sean cualitativamente tan poderosas como las computadoras cuánticas. Por lo tanto, este trabajo proporciona un argumento convincente de que este algoritmo ofrece una aceleración exponencial, así como una clara demostración de un vínculo novedoso y sutil entre la dinámica cuántica y el humilde oscilador armónico.
"Se han desarrollado muy pocas clases nuevas de aceleraciones exponenciales demostrables de los cálculos clásicos", dijo Wiebe. "Nuestro trabajo proporciona una ventaja computacional significativa para una amplia gama de problemas en ingeniería, neurociencia y química".
Más información: Ryan Babbush et al, Aceleración cuántica exponencial en la simulación de osciladores clásicos acoplados, Revisión física X (2023). DOI:10.1103/PhysRevX.13.041041
Información de la revista: Revisión física X
Proporcionado por el Laboratorio Nacional del Noroeste del Pacífico