Una nueva publicación de Opto-Electronic Advances considera la investigación sobre estados topológicos de cristales fotónicos más allá del límite de difracción óptica.

La luz omnipresente muestra diferentes características en diferentes materiales. Si el material se dispone periódicamente de forma selectiva al nivel de longitud de onda de la luz, provocando regiones repetidas regularmente de constante dieléctrica alta y baja, se puede controlar el comportamiento de propagación de la luz. Estas estructuras periódicas se denominan cristales fotónicos y las longitudes de onda que se propagan se denominan modos. Basado en cristal fotónico, hay muchas aplicaciones, como recubrimientos de baja y alta reflexión en lentes y espejos, fibras de cristal fotónico, sensores ópticos, etc.

Una de las mayores dificultades en el proceso de fabricación de cristales fotónicos es el defecto, que puede provocar la dispersión de la luz que se propaga en los cristales fotónicos. Estos defectos son difíciles de evitar, ya que siempre hay algunas imperfecciones en el proceso de fabricación. Para superar este problema, la topología como concepto matemático que se ocupa de las propiedades invariantes bajo deformación continua se introdujo en la fotónica para describir la propiedad global de los cristales fotónicos. Los cristales fotónicos topológicos se centran en las características generales y no son sensibles a los defectos locales. Y si el cristal fotónico es topológico no trivial, admite estados ópticos en su límite, que tampoco son sensibles a los defectos locales. Estos sólidos estados límite pueden permitir excelentes aplicaciones para la comunicación óptica y las emisiones cuánticas, como la guía de ondas unidireccional y el láser monomodo.

Sin embargo, debido al límite de difracción de la luz, es difícil obtener detalles de los estados ópticos con una longitud característica de alrededor de 300 nm o menos. Algunos fenómenos físicos novedosos no se han estudiado por completo mediante el uso de microscopía óptica tradicional, como una línea oscura que existe con el estado de borde topológico protegido por simetría cristalina.

Recientemente, el grupo de investigación del profesor Zheyu Fang de la Universidad de Pekín mostró una investigación sobre el estado del borde topológico del cristal fotónico. En esta investigación, el límite de difracción óptica se rompe mediante el uso de la nanoscopia de catodoluminiscencia (CL). La línea oscura se refleja con una resolución de sublongitud de onda profunda y el mecanismo de la línea oscura se aclara con la distribución del campo electromagnético que se calcula mediante simulación numérica. Su investigación proporciona una comprensión más profunda de los estados de borde topológicos y puede tener una gran importancia para el diseño de futuros dispositivos topológicos en chip.

El grupo de investigación del profesor Zheyu Fang de la Universidad de Pekín realizó el Z₂ estado de borde topológico en el rango visible y caracteriza su línea oscura con la nanoscopia de catodoluminiscencia (CL). Su estructura se compone de una región de cristal fotónico trivial topológico externo y una región de cristal fotónico no trivial topológico interno. El estado de borde topológico está confinado en la interfaz entre estos dos tipos de cristales fotónicos.

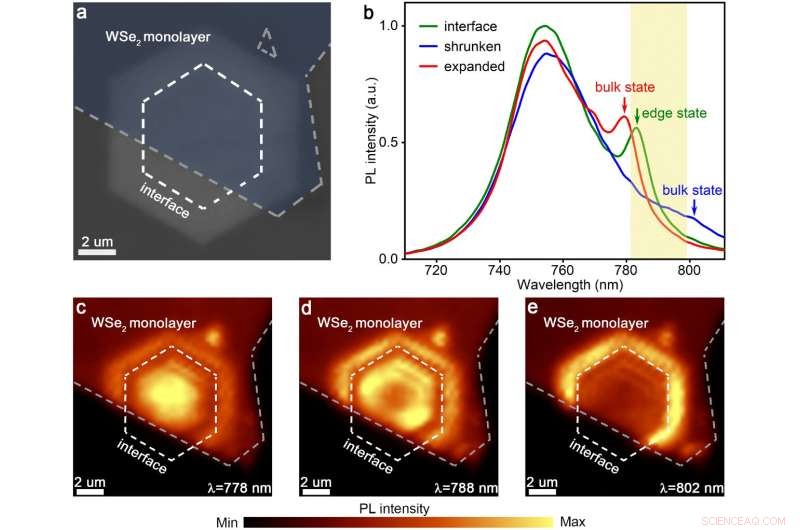
El estado del borde topológico se refleja directamente desde la estructura de cristal fotónico diseñada con la fotoluminiscencia mejorada (PL) del WSe₂ monocapa que cubrió en la parte superior. La densidad local óptica radiativa de los estados del estado de borde se caracteriza aún más mediante el uso de nanoscopía CL con una resolución de alrededor de 10 nm, rompiendo el límite de difracción óptica. Se encuentra que la línea oscura del estado de borde está exactamente localizada en la región vecina de la celda unitaria no trivial cerca de la interfaz.

Y la línea oscura se interpreta con la distribución del campo orbital p-d artificial analizando en detalle los estados de borde topológicos simulados. Descubrieron que la energía del Z₂ El estado del borde topológico se localiza en la interfaz y decae gradualmente en el área vecina, mientras que las proporciones de los orbitales p y d son diferentes según las distancias a la interfaz. Esto conduce a diferentes características de radiación del Z₂ estados de borde topológicos en diferentes posiciones. Las líneas oscuras en la región vecina de la celda unitaria no trivial cerca de la interfaz están compuestas principalmente de componentes orbitales d, por lo que la radiación del Z₂ el estado del borde topológico es débil en esta región.

Esto se puede usar directamente para mejorar la eficiencia cuántica del láser de estado de borde topológico (componente orbital p) o inhibir la emisión cuántica (componente orbital d). Además, esta caracterización CL resuelta en sublongitud de onda profunda se puede adaptar a cualquier otro análisis de modo topológico fotónico. Este trabajo fortalece la comprensión detallada de Z₂ Los estados de borde topológicos y constituyen una instrucción vital para la exploración y el diseño de dispositivos topológicos en chip, lo que beneficia el desarrollo de la comunicación óptica y la óptica cuántica del futuro.

En el campo de la fotónica micro-nano, el grupo de investigación del Prof. Zheyu Fang de la Universidad de Pekín se centra en las teorías, materiales, aplicaciones, diseños de IA y métodos de caracterización de catodoluminiscencia. Estudiaron la preparación y caracterización de nanoestructuras plasmónicas, el enfoque óptico a nanoescala y el diseño de guías de ondas, el dopaje y la detección de interfaces de electrones calientes, el comportamiento de excitones de materiales bidimensionales y las características de luminiscencia, etc. Se han logrado muchos resultados de investigación innovadores en cuestiones científicas clave. como la miniaturización de fotodetectores de alta eficiencia y la modulación de las características fotoeléctricas de las estructuras plasmónicas bajo el campo externo. + Explora más

Nanoláseres topológicos de umbral bajo basados ​​en el estado de esquina de segundo orden