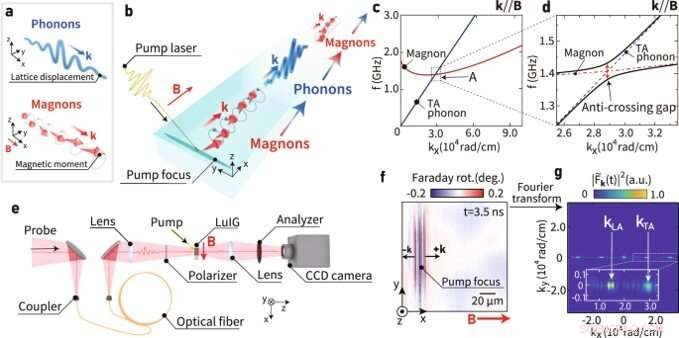
Oscilación coherente entre fonones y magnones

Concepto de oscilación coherente entre fonones y magnones, y microscopía magnetoóptica resuelta en el tiempo. (a) Una ilustración esquemática de fonones y magnones, (b) Una ilustración esquemática de oscilación coherente entre fonones y magnones. ( c ) Las curvas de dispersión de fonón y magnón en granate de hierro lutecio (LuIG). ( d ) Una vista ampliada alrededor de A en la Fig. 1c. Las curvas negras representan la relación de dispersión del polarón magnón-fonón híbrido, mientras que las curvas discontinuas rojas y azules representan la relación de dispersión de los magnones puros y los fonones acústicos transversales, respectivamente. ( e ) Configuración óptica para la microscopía magneto-óptica resuelta en el tiempo con el tiempo de retardo extendido. La dinámica de magnetización excitada se detecta a través del ángulo de rotación de polarización del pulso láser de la sonda inducido por el efecto magneto-óptico de Faraday en la muestra. La detección se realiza mediante una cámara de dispositivo de carga acoplada (CCD). (f) Imagen magnetoóptica observada 3,5 ns después de la irradiación del pulso de la bomba bajo el campo magnético externo B = 11,5 mT paralelo al vector de onda de los magnones excitados. g, Espectro de número de onda de las imágenes magnetoópticas obtenidas observadas 3,5 ns después de la excitación (B = 11,5 mT). El recuadro muestra una vista ampliada. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00888-1

Se pueden acoplar dos ondas diferentes con la misma frecuencia y longitud de onda, de modo que la amplitud alterna periódicamente entre las dos para formar un fenómeno conocido como oscilación de latido coherente. El proceso se puede observar a menudo con un péndulo acoplado ya escala cósmica como oscilaciones de neutrinos que ocurren debido a fluctuaciones entre diversos neutrinos. Los sólidos también pueden mantener diversas excitaciones de ondas para contribuir a sus propiedades térmicas y electromagnéticas.

En un nuevo informe publicado ahora en Nature Communications Physics , Tomosato Hioki y un equipo de científicos en investigación de materiales y física aplicada en la Universidad de Tohoku y la Universidad de Tokio en Japón, describieron latidos coherentes observados entre diferentes especies de excitación en un sólido, a saber, fonones (energía mecánica vibratoria cuántica) y magnones (un cuasipartícula que representa la excitación colectiva de la estructura de espín del electrón. El equipo usó microscopía magneto-óptica de resolución temporal para mostrar cómo los magnones generados en un compuesto desaparecían gradualmente al transferirse a fonones, para luego volver a la forma de magnones después de un tiempo. El período de oscilación fue consistente con el latido magnón-fonón. Los científicos prevén que los resultados experimentales allanarán el camino para controlar coherentemente los sistemas magnón-fonón en los sólidos.

Interacciones fonón-magnón en granate de hierro lutecio

Los fonones son ondas vibratorias de una red cristalina sólida responsables de la elasticidad y las propiedades térmicas de los sólidos. Los magnones u ondas de espín son, por el contrario, representativos de un movimiento ondulatorio de magnetización, presente en los imanes responsables de sus propiedades magnéticas y térmicas. Estas dos partículas pueden interactuar dentro de los sólidos a través de acoplamientos magneto-elásticos y magneto-estáticos. La dinámica de las partículas se proporciona en las curvas de dispersión de cada sistema para mostrar la relación entre el número de onda y la frecuencia. Los científicos han registrado las curvas de dispersión de fonones y magnones acústicos transversales en una película de un aislante típico como el granate de hierro lutecio. Tales curvas de dispersión de las partículas de fonón y magnón mantienen una intersección alrededor de la cual se puede formar un estado hibridado magnón-fonón. Los investigadores han descubierto que este estado exhibe una vida útil extremadamente larga, mucho mayor que los magnones puros debido a la hibridación con fonones que mantienen una vida útil prolongada.

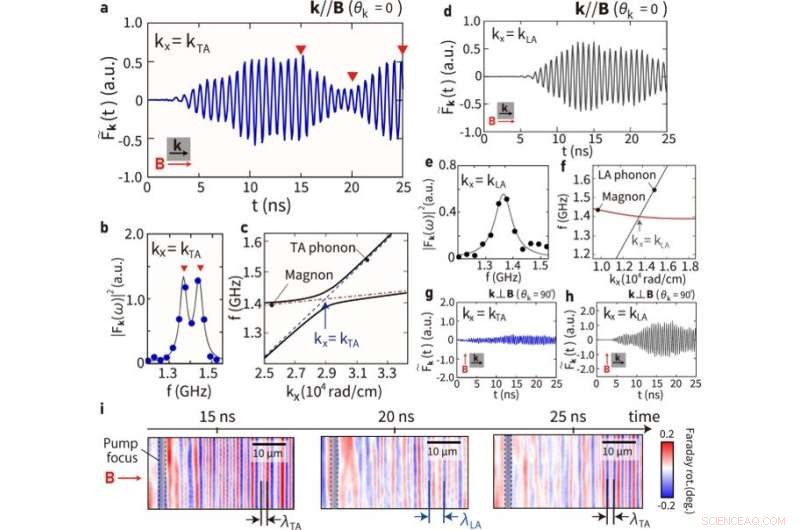
Observación de la oscilación coherente magnón-fonón. (a) Evolución temporal de la parte real de F~k(t) en kx = kTA bajo el campo magnético B = 11.5 mT paralelo a k, donde kTA se refiere al número de onda del punto de intersección entre las relaciones de dispersión de la acústica transversal (TA ) fonones y magnones. Los triángulos rojos invertidos indican t = 15 ns, 20 ns y 25 ns después de la irradiación del pulso de la bomba. (b) Un espectro de potencia de frecuencia de F~k(t) en kx = kTA. Los círculos rellenos de azul representan la intensidad del espectro obtenido experimentalmente, mientras que la curva gris representa la curva de ajuste. El triángulo rojo invertido resalta los picos. Los errores de los datos se evalúan como una desviación estándar, que es más pequeña que la gráfica de datos. (c) Curvas de dispersión calculadas teóricamente de polarones de magnón alrededor de kx = kTA y ky = 0, donde usamos la energía de anisotropía cristalina Kc = 73.0 [J ⋅ m−3], energía de anisotropía uniaxial Ku = −767.5 [J ⋅ m−3 ], magnetización de saturación Ms = 14.8 [kA ⋅ m−1], velocidad de LA fonones vLA = 6.51 [km ⋅ s−1], velocidad de TA fonones vTA = 3.06 [km ⋅ s−1] y constante de acoplamiento magnón-fonón b2 = 1.8 × 105 [J ⋅ m−3]. Las curvas continuas negras representan las curvas de dispersión de los polarones magnon, mientras que las curvas discontinuas azules y rojas representan fonones TA puros y magnones, respectivamente. (d) Evolución temporal de la parte real de F~k(t) en kx = kLA bajo el campo magnético B = 11.5 mT paralelo a k, donde kLA se refiere al número de onda del punto de intersección entre las relaciones de dispersión de la acústica longitudinal (LA ) fonones y magnones. (e) Un espectro de potencia de frecuencia de F~k(t) en kx = kLA. Los círculos negros representan la intensidad del espectro obtenida experimentalmente, mientras que la curva gris representa la curva de ajuste. Los errores de los datos se evalúan como una desviación estándar, que es más pequeña que la gráfica de datos. (f) Curvas de dispersión calculadas teóricamente de polarones de magnón alrededor de kx = kLA. La línea gris y la curva roja representan las curvas de dispersión de los fonones y magnones LA, respectivamente. (g) Evolución temporal de la parte real de F~k(t) en kx = kTA bajo el campo magnético B = 11.5 mT perpendicular a k. (h) Evolución temporal de la parte real de F~k(t) en kx = kLA bajo el campo magnético B = 11.5 mT perpendicular a k. (i), Imágenes magneto-ópticas tomadas en diferentes tiempos de retardo. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00888-1

Los físicos han confirmado la vida útil prolongada en el granate de hierro de lutecio, mientras miden la conversión de calor de espín, incluso a temperatura ambiente. Los investigadores esperan observar simultáneamente una superposición coherente que forme una oscilación de latido correspondiente entre fonones y magnones. En este trabajo, Hioki et al describieron la observación de latidos coherentes entre dos fonones y magnones dentro del granate de hierro lutecio. El equipo utilizó microscopía magnetoóptica de resolución temporal y midió la dinámica de magnetización. Descubrieron el latido coherente de hasta decenas de nanosegundos y confirmaron experimentalmente un fuerte acoplamiento entre magnones y fonones en la película desnuda de granate de hierro lutecio, abreviado como LUIG.

La configuración experimental

Hioki et al exploraron las oscilaciones de los sólidos mediante el desarrollo del microscopio magnetoóptico de resolución temporal. Durante los experimentos, utilizaron una película delgada de LUIG con un grosor de 1,8 µm, con grandes efectos magnetoópticos y una pequeña amortiguación de magnetización. El equipo excitó la dinámica de magnetización al enfocar una luz láser pulsada con una longitud de onda de 800 nm en la muestra, que correspondía a casi la mitad de la energía de la banda prohibida de LUIG. La bomba excitó la onda de espín o los magnones a través de la desmagnetización fotoinducida y la expansión fotoinducida. Los científicos excitaron selectivamente el magnón perpendicular a la línea vertical utilizando interferencias de Huygens-Fresnel. A partir de entonces, utilizaron otro pulso de luz débil, conocido como pulso de sonda en la muestra con una longitud de onda de 630 nm, y midieron la distribución espacial de la rotación magneto-óptica de Faraday del pulso de sonda transmitido a través de la muestra a través de una cámara. El equipo resolvió la frecuencia de la brecha magnón-fonón en la muestra durante los experimentos.

Número de onda y dependencia del campo de la oscilación coherente magnón-fonón. (a) Espectro de frecuencia Fk(ω) observado en B = 11,5 mT alrededor de la intersección de las curvas de dispersión de fonones magnón y acústica transversal (TA). (b) Comparación entre la brecha obtenida experimentalmente entre la rama superior y la rama inferior del espectro en B = 11.5 mT y el cálculo teórico de la frecuencia de la brecha. Las barras de error representan la desviación estándar. (c) Espectro de frecuencia Fk(ω) observado en B = 13,0 mT alrededor de la intersección de las curvas de dispersión de magnón y TA-fonón. (d) Comparación entre la brecha obtenida experimentalmente entre la rama superior y la rama inferior del espectro de frecuencia en B = 13.0 mT y el cálculo teórico de la frecuencia de la brecha. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00888-1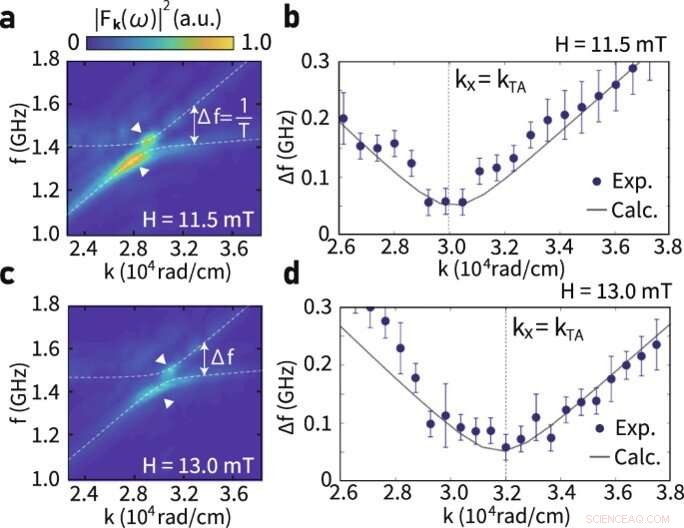

Oscilaciones coherentes entre fonones y magnones

El equipo obtuvo un ángulo de rotación de polarización después de la irradiación de pulso de bomba, donde aparecieron patrones de ondas verticales en las cercanías del foco del pulso de bomba para demostrar la excitación magnónica del dispositivo. Confirmaron que la rotación de la polarización se debe al efecto magneto-óptico de Faraday. Los resultados mostraron el desarrollo de polarones de magnones en la intersección de las curvas de dispersión de magnones y fonones después de la irradiación de pulsos de bomba. Hioki et al midieron directamente los magnones puros mediante microscopía para mostrar la señal que oscila periódicamente en función del tiempo con la frecuencia de los magnones.

Luego midieron la rotación magneto-óptica de Faraday y mostraron la desaparición de la señal cuando los magnones se transformaban en fonones. Las oscilaciones observadas implicaban latidos periódicos entre magnones y fonones en el dominio del tiempo. El equipo demostró además las oscilaciones de latido coherentes en el espacio real a través del cambio oportuno en el patrón de onda excitado por el pulso de la bomba. Discutieron los espectros de excitación de los magnones y la frecuencia de oscilación coherente, así como la frecuencia angular en la intersección entre las curvas de distribución de magnones y fonones. Los resultados mostraron un buen acuerdo con los cálculos teóricos.

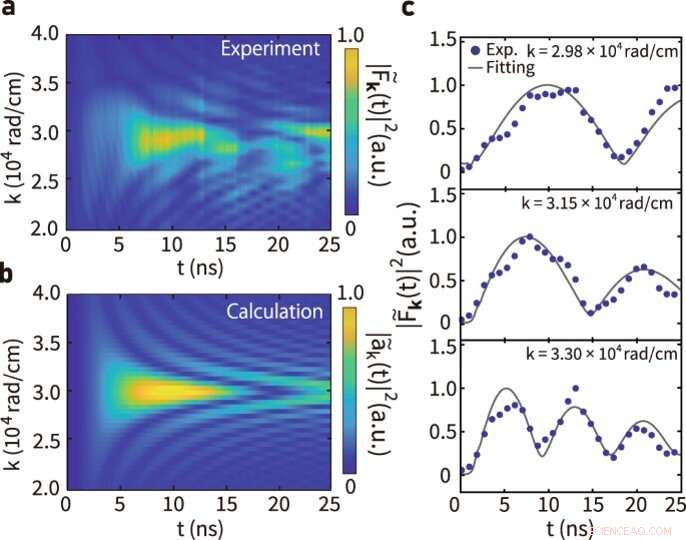
Ajuste de parámetros de oscilación coherente. (a) Evolución temporal obtenida experimentalmente de |F~k(t)|2 en B = 11.5 mT. (b) Evolución temporal calculada de la amplitud del magnón |a~k(t)|2. (c) Evolución temporal de |F~k(t)|2 en diferentes números de onda. Las curvas grises representan curvas de ajuste de acuerdo con la ecuación. (3) descrito en el estudio. Los errores de los datos se evalúan como una desviación estándar, que es más pequeña que la gráfica de datos. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00888-1

Cálculo numérico de la intensidad de excitación del magnón. (a) Mapa de calor de G(r). σx y σy están configurados para realizar la excitación de onda plana de magnon polaron (σx = 40 nm, σy = 40 nm). ( b ) Evolución temporal de la intensidad de excitación f (t). ( c ) Mapa de calor de la intensidad del espectro calculado de acuerdo con la ecuación. (ts = 1.5 ns, te = 1.6 ns, σt = 0.3 ns). La intensidad del espectro alcanza su punto máximo en el cruce de dispersión entre el fonón acústico transversal (TA) y el magnón, reproduciendo los resultados experimentales. Crédito:Física de las comunicaciones (2022). DOI:10.1038/s42005-022-00888-1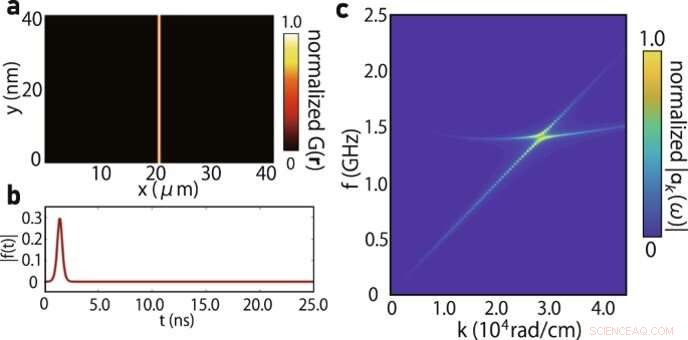

Perspectiva

De esta manera, Tomosato Hioki y sus colegas midieron numéricamente la evolución temporal de la amplitud del magnón calculando la transformada de Fourier de la amplitud espectral del magnón. El equipo consideró que la dinámica acoplada entre los fonones acústicos transversales y los magnones era relevante para la oscilación observada. Para comprender los resultados experimentales, Hioki et al atribuyeron la gran cooperatividad a la pequeña amortiguación magnética intrínseca y al factor de alta calidad de los fonones en los cristales de granate. Los científicos mejoraron aún más el acoplamiento magnón-fonón en la película al fabricar cristales fonónicos o magnónicos a partir de la película plana, para ayudar al control de los magnones en los circuitos y dispositivos magnónicos. Las oscilaciones coherentes magnón-fonón presentadas proporcionan una plataforma para estudiar la dinámica de los sistemas acoplados, para regular las propiedades magnéticas y elásticas en una variedad de materiales magnéticos. + Explora más