En geometría, un octágono es un polígono con ocho lados. Un octágono regular tiene ocho lados iguales y ángulos iguales. El octágono regular se reconoce comúnmente a partir de los signos de alto. Un octaedro es un poliedro de ocho lados. Un octaedro regular tiene ocho triángulos con bordes de igual longitud. En realidad se trata de dos pirámides cuadradas que se encuentran en sus bases.
Octágono Fórmula de área
La fórmula para el área de un octágono regular con lados de longitud "a" es 2 (1 + sqrt (2) )) a ^ 2, donde "sqrt" indica la raíz cuadrada.
Derivación
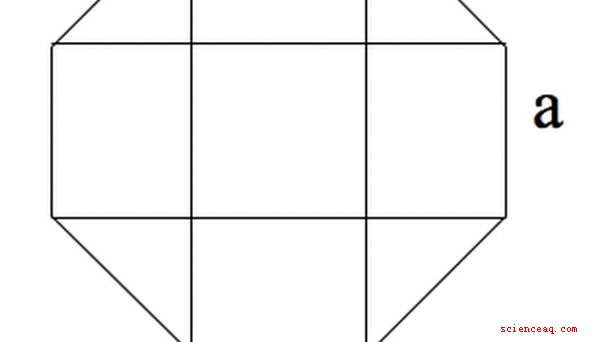
Un octágono se puede ver como 4 rectángulos, un cuadrado en el centro y cuatro triángulos isósceles en las esquinas.
El cuadrado es del área a ^ 2.
Los triángulos tienen lados a, a /sqrt (2) y a /sqrt (2), según el teorema de Pitágoras. Por lo tanto, cada uno tiene un área de ^ 2/4.
Los rectángulos son del área a * a /sqrt (2).
La suma de estas 9 áreas es 2a ^ 2 ( 1 + sqrt (2)).
Octahedron Volume Formula
La fórmula para el volumen de un octaedro regular de lados "a" es un ^ 3 * sqrt (2) /3.
Derivación
El área de una pirámide de cuatro lados es el área de base * altura /3. El área de un octágono regular es por lo tanto 2 * base * altura /3.
Base = a ^ 2 trivial.
Elija dos vértices adyacentes, digamos "F" y "C". "O" está en el centro. FOC es un triángulo rectángulo isósceles con la base "a", por lo que OC y OF tienen longitud a /sqrt (2) según el teorema de Pitágoras. Entonces height = a /sqrt (2).
Entonces el volumen de un octaedro regular es 2 * (a ^ 2) * a /sqrt (2) /3 = a ^ 3 * sqrt (2) /3.
Área de superficie
La superficie de octaedro regular es el área de un triángulo equilátero de lado "a" por 8 caras.
Para usar el teorema de Pitágoras, coloca una línea desde el ápice hasta la base. Esto crea dos triángulos rectángulos, con la hipotenusa de longitud "a" y una longitud lateral "a /2". Por lo tanto, el tercer lado debe ser sqrt [a ^ 2 - a ^ 2/4] = sqrt (3) a /2. Entonces el área de un triángulo equilátero es altura * base /2 = sqrt (3) a /2 * a /2 = sqrt (3) a ^ 2/4.
Con 8 lados, el área superficial de un octaedro regular es 2 * sqrt (3) * a ^ 2.