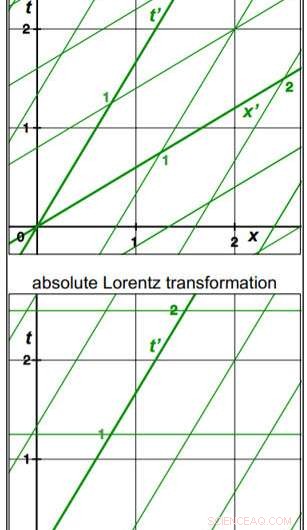
Crédito:World Scientific Publishing
Uno de los aspectos estructurales más básicos del espacio-tiempo relativista es la descripción de cómo el movimiento altera el tiempo y las distancias. La teoría de la relatividad especial describe un marco de espacio-tiempo para el movimiento lineal constante en el que el tiempo se dilata y las longitudes se contraen en respuesta al movimiento. Este marco es descrito por la transformación de Lorentz, que abarca fórmulas matemáticas que describen cómo se alteran el tiempo y la distancia entre marcos de referencia en movimiento. La transformación de Lorentz también describe cómo un observador estacionario ve el tiempo en el marco en movimiento para compensarlo con la distancia. La compensación del tiempo con la distancia entre los marcos de referencia genera simultaneidad diferencial, en el que los eventos que son simultáneos para un observador no lo serán para un segundo observador que se mueve en relación con el primer observador.
La naturaleza del espacio-tiempo en marcos rotativos no se ha establecido en el nivel más fundamental de definir la transformación que describe con precisión los efectos relativistas y el marco de simultaneidad. Hay cuatro transformaciones relativistas rotacionales distintas en la literatura:la métrica de Langevin; Post transformación; Transformación de Franklin; y la transformación de Lorentz absoluta (ALT) en su forma rotacional. Determinar qué transformación describe con precisión los datos experimentales indicaría el marco del espacio-tiempo que está presente en los marcos giratorios del mundo real. Comprender esta información fundamental tiene una amplia aplicabilidad porque la mayoría de la materia visible en el Universo está en movimiento de rotación, incluida la Tierra en rotación.
La transformación rotacional más citada es la métrica de Langevin, que se describió por primera vez en 1921. A lo largo de las décadas, la métrica de Langevin se ha utilizado para describir la relatividad en marcos rotativos en cientos de libros de texto y artículos de investigación. Sin embargo, la métrica de Langevin nunca se ha evaluado con datos experimentales que tengan suficiente resolución para distinguirla de las otras transformaciones rotacionales importantes.
La combinación de una transformación de efectos relativistas y un marco de simultaneidad afecta cómo se propaga la luz. Las cuatro transformaciones tienen diferentes predicciones para las velocidades unidireccionales de la luz del marco giratorio, velocidad bidireccional de la luz, y el efecto Sagnac. Este estudio deriva las predicciones ópticas para cada transformación directamente de sus ecuaciones de transformación, con varias de las predicciones no reportadas previamente en la literatura. A continuación, las predicciones se comparan con datos experimentales ópticos de alta resolución recientes.
Los datos del resonador óptico sobre la velocidad bidireccional de la luz se encuentran entre las mediciones científicas de mayor resolución, con resoluciones de 10 -18 . Esta alta resolución es necesaria para distinguir entre las predicciones de las transformaciones. El estudio revela que ALT y la predicción de transformación de Franklin de la velocidad bidireccional constante de la luz, C, coincide con los datos del resonador óptico, mientras que la métrica de Langevin y las predicciones posteriores a la transformación son invalidadas por los datos. Se muestra que el fallo de la métrica de Langevin y la transformación posterior para coincidir con los datos del resonador óptico se debe a que no presentan contracción de longitud (o neta) en el marco giratorio. A diferencia de, las transformaciones ALT y Franklin exhiben una contracción de la longitud, lo que permite sus predicciones precisas de la velocidad bidireccional de la luz.
Datos sobre el efecto Sagnac, que tiene resoluciones más bajas de 10 -8 , es compatible con las predicciones del efecto Sagnac de la métrica de Langevin, Correo, y transformaciones ALT, pero es incompatible con la transformación de Franklin, que no predice ningún efecto Sagnac. Se muestra que el fracaso de la transformación de Franklin para generar un efecto Sagnac manifiesto se debe a su incorporación de simultaneidad diferencial. A diferencia de, las otras tres transformaciones incorporan simultaneidad absoluta en la que el tiempo no se compensa con la distancia, que permite efectos Sagnac abiertos. Por lo tanto, ALT es la única transformación que describe con precisión la gama completa de datos ópticos relativistas.
Múltiples publicaciones han propuesto mecanismos para incorporar simultaneidad diferencial en marcos rotativos para permitir la generación de un efecto Sagnac manifiesto. Sin embargo, estos mecanismos generan ecuaciones alternas del efecto Sagnac. El estudio muestra que estas ecuaciones alternativas del efecto Sagnac implican velocidades de luz bidireccionales que son invalidadas por los datos del resonador óptico de alta resolución. A diferencia de, ALT predice el efecto Sagnac convencional, lo que implica la constante velocidad bidireccional de la luz, C.
El estudio demuestra que la transformación rotacional ALT predice con precisión tanto datos ópticos de alta resolución como observaciones relativistas de marco giratorio no óptico. Este análisis implica que la transformación rotacional ALT describe el marco básico del espacio-tiempo en marcos rotativos. Esto aclara que el espacio-tiempo de marco giratorio se caracteriza por los efectos relativistas de la dilatación del tiempo y la contracción de la longitud dentro de un marco de simultaneidad absoluta en el que el tiempo no se compensa con la distancia.