
El robot Slinky. (A) Esquema que muestra el mecanismo locomotor de una lombriz de tierra basado en ondas peristálticas retrógradas (es decir, ondas que se propagan en dirección opuesta a la locomoción). (B) Imagen del Slinky metálico utilizado en este estudio. (C y D) Imágenes de nuestro robot Slinky (C) antes y (D) después de que se alargue el actuador neumático. (E) Vista frontal del robot Slinky que muestra el electroimán. Tenga en cuenta que varias esferas de plástico rojas están pegadas al Slinky para evitar que ruede. Crédito de la foto:Bolei Deng, Universidad Harvard. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1166
Los científicos han explorado recientemente las propiedades únicas de las ondas no lineales para facilitar una amplia gama de aplicaciones, incluida la mitigación de impactos, transmisión asimétrica, conmutación y enfoque. En un nuevo estudio ahora publicado en Avances de la ciencia , Bolei Deng y un equipo de científicos de investigación de Harvard, El CNRS y el Instituto Wyss de Ingeniería de Inspiración Biológica en los EE. UU. Y Francia aprovecharon la propagación de ondas no lineales para hacer que las estructuras flexibles se arrastraran. Combinaron métodos experimentales y teóricos bioinspirados para mostrar cómo tal locomoción impulsada por pulsos podía alcanzar una eficiencia máxima cuando los pulsos iniciados eran solitones (onda solitaria). La máquina simple desarrollada en el trabajo podía moverse a través de una amplia gama de superficies y seguir adelante. El estudio amplió la variedad de posibles aplicaciones con ondas no lineales para ofrecer una nueva plataforma para máquinas flexibles.
Las estructuras flexibles que son capaces de grandes deformaciones están atrayendo el interés de la bioingeniería debido a su intrigante respuesta estática y su capacidad para soportar ondas elásticas de gran amplitud. Controlando cuidadosamente su geometría, El panorama de energía elástica de los sistemas altamente deformables se puede diseñar para propagar una variedad de ondas no lineales, incluidos los solitones vectoriales, ondas de transición y pulsos de rarefacción. El comportamiento dinámico de tales estructuras demuestra una física muy rica, al tiempo que ofrece nuevas oportunidades para manipular la propagación de señales mecánicas. Tales mecanismos pueden permitir la propagación unidireccional, guía de olas, lógica mecánica y mitigación, entre otras aplicaciones.
En este trabajo, Deng y col. se inspiraron en el movimiento de ondas peristálticas retrógradas biológicas en las lombrices de tierra y en la capacidad de las ondas elásticas lineales para generar movimiento en motores ultrasónicos. El equipo mostró la propagación de ondas elásticas no lineales en estructuras flexibles para brindar oportunidades de locomoción. Como prueba de concepto, se centraron en un Slinky y lo utilizaron para crear un robot impulsado por pulsos capaz de impulsarse a sí mismo. Construyeron la máquina simple conectando el Slinky a un actuador neumático. El equipo usó un electroimán y una placa incrustados entre los bucles para iniciar pulsos no lineales que se propagarán a lo largo del dispositivo de adelante hacia atrás. permitiendo que la direccionalidad del pulso dicte que el robot simple avance. Los resultados indicaron que la eficiencia de tal locomoción impulsada por pulsos era óptima con solitones:pulsos no lineales de gran amplitud con una velocidad constante y una forma estable a lo largo de la propagación. El estudio amplió las aplicaciones de ondas solitarias (solitones) al tiempo que muestra cómo se pueden explorar como motores subyacentes simples para ayudar a las máquinas flexibles a moverse.
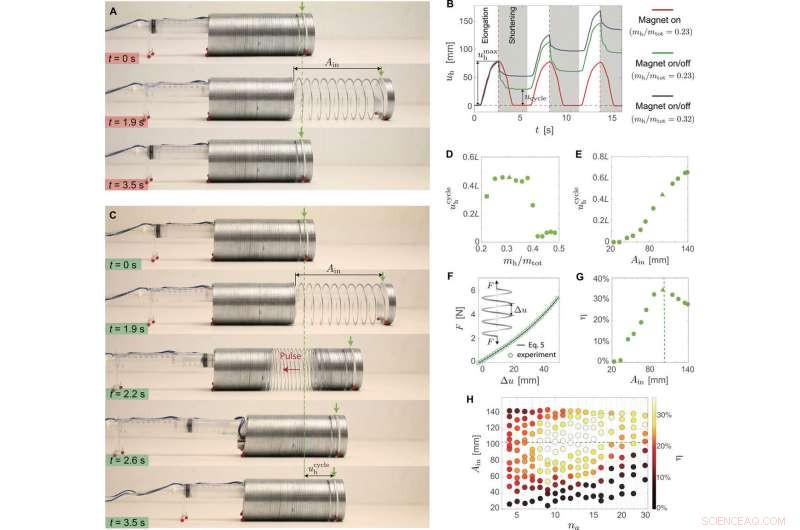
Rendimiento del robot Slinky. (A) Instantáneas tomadas durante una prueba en la que extendimos los 10 bucles frontales a Ain =100 mm mientras mantenemos el electroimán encendido. (B) Desplazamiento del cabezal durante tres ciclos para pruebas en las que (i) mh / mtot =0.23 y mantenemos el electroimán encendido (línea roja), (ii) mh / mtot =0.23 y apagamos el electroimán después de estirar (línea verde), y (iii) mh / mtot =0.32 y apagamos el electroimán después de estirar (línea azul). (C) Instantáneas tomadas durante una prueba en la que Ain =100 mm y apagamos el electroimán después de estirar los bucles frontales. (D) Evolución del ciclo u h en función de mh / mtot para ensayos en los que Ain =100 mm. Los marcadores cuadrados y triangulares corresponden a mh / mtot =0.23 y 0.32, respectivamente. (E) Evolución del ciclo u h en función de Ain para pruebas en las que mh / mtot =0.32. El marcador triangular corresponde a Ain =100 mm. (F) Respuesta estática del Slinky medida en una prueba uniaxial. (G) Evolución de η en función de Ain para pruebas en las que mh / mtot =0.32. Los marcadores triangulares corresponden a Ain =100 mm. La línea punteada verde corresponde a la amplitud del solitón soportado, Como. (H) Evolución de η en función de na y Ain para pruebas en las que mh / mtot =0.32. Crédito de la foto:Bolei Deng, Universidad Harvard. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1166
Para crear el robot Slinky, Deng y col. usó un Slinky de metal con una longitud de 50 mm y 90 bucles, para luego probar y comprender cómo explorar su flexibilidad intrínseca, y crear una máquina sencilla capaz de moverse. Conectaron dos slinkies en serie (100 mm, 180 lazos) para una estrategia de actuación sencilla basada en un actuador neumático, un electroimán y tres placas acrílicas. Podrían estirar y acortar la configuración utilizando el actuador neumático mientras mantienen el electroimán encendido. El equipo probó la respuesta de la máquina colocándola sobre una superficie lisa y monitoreándola con una cámara de alta velocidad. Deng y col. luego apagó el campo magnético en un intento de romper la simetría y hacer que la máquina se arrastrara. No observaron una onda reflejada en el Slinky debido a la gran disipación de energía tras la colisión de los bucles y, en cambio, observaron un claro movimiento hacia adelante del robot. Por lo tanto, el equipo exploró la direccionalidad introducida por las ondas elásticas para hacer que el robot se mueva, incluso en presencia de coeficientes de fricción idénticos.

Propagación de ondas no lineales. Un slinky con 90 bucles se levanta del sustrato y se sostiene con una varilla de plástico para minimizar la fricción. Al estirar previamente 10 bucles cerca del frente y apagar el electroimán magnético, iniciamos ondas elásticas que se propagan hacia la parte posterior. Los marcadores verdes se utilizan para rastrear el desplazamiento de todos los demás bucles. Ver película completa en Crédito:Science Advances, doi:10.1126 / sciadv.aaz1166
Sin embargo, los intentos de hacer que la máquina flexible se arrastre mediante pulsos elásticos revelaron que las condiciones experimentales no eran óptimas. Por ejemplo, notaron un retroceso inmediatamente después de apagar el electroimán. Para limitar este movimiento, Deng y col. aumentó la masa en la cabeza del robot Slinky mientras optimizaba el valor para identificar un rango óptimo. El Slinky mantuvo 10 bucles entre las placas frontal y de carga en la configuración. El equipo designó la distancia máxima entre la carga y las placas frontales como A en , que aproximó 100 mm. Para comprender cómo la eficiencia del robot fue máxima para A en =100 mm Deng y col. investigó cuidadosamente la propagación de pulsos de gran amplitud a través del Slinky.
Para estos experimentos, se enfocaron en un solo Slinky y monitorearon la posición de los marcadores verdes ubicados en cada otro bucle. Luego iniciaron ondas elásticas que se propagaron hacia la parte posterior estirando previamente 10 bucles cerca del frente y apagando el electroimán. Las pruebas permitieron al equipo recopilar información más profunda sobre la propagación de pulsos al monitorear el desplazamiento de cada bucle. Los científicos se dieron cuenta de dos características principales del robot; 1) las ondas que se propagan hacia atrás movieron el centro de masa del Slinky hacia adelante y 2) el Slinky apoyó la propagación de ondas solitarias de gran amplitud.

Para na =4 los pulsos son demasiado fuertes, y su energía se disipa a través de colisiones entre los bucles. Para na =30, los pulsos son demasiado débiles y apenas se propagan. Ver película completa en Crédito:Science Advances, doi:10.1126 / sciadv.aaz1166
Para obtener más información sobre los resultados experimentales, Deng y col. desarrolló un modelo matemático que representaba la masa y elasticidad de un bucle individual. Los resultados calculados coincidieron extremadamente bien con los resultados experimentales y el modelo confirmó las observaciones experimentales. El análisis confirmó además que la eficiencia del robot Slinky estaba al máximo cuando las ondas iniciadas eran solitones. La naturaleza no dispersiva y la compacidad de los pulsos solitarios los hicieron extremadamente eficientes para transferir la energía proporcionada por el actuador neumático en movimiento con el fin de obtener la locomoción impulsada por pulsos más eficiente.
De este modo, Deng y col. mostró cómo los solitones que se propagaban hacia atrás podían mover eficientemente un robot Slinky hacia adelante. A pesar de que los organismos sin extremidades han bioinspirado previamente a ingenieros para diseñar una variedad de robots, el equipo cree que este trabajo es el primer sistema robótico que depende de pulsos elásticos para moverse. Los principios presentados en el estudio fueron diferentes a los utilizados por los motores ultrasónicos, Dado que el robot Slinky flexible usó ondas de pulso no lineales para cambiar la posición del centro de masa, Los motores ultrasónicos, por el contrario, funcionan con ondas lineales sinusoidales. El equipo solo se centró en el avance rectilíneo en este trabajo, pero pueden explorar la flexibilidad del Slinky para lograr una variedad de movimientos.
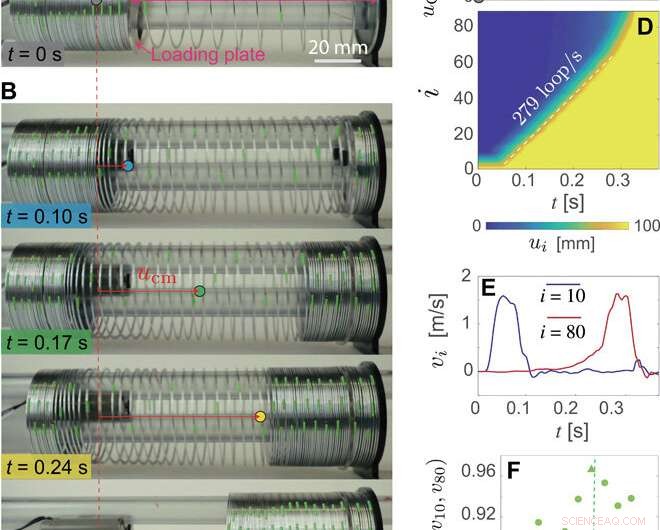
Propagación de ondas en el Slinky. (A) Configuración experimental utilizada para probar la propagación de pulsos en el Slinky metálico. En t =0 s, na =10 bucles entre la placa de carga y la parte delantera del Slinky se estiran a Ain =100 mm. (B) Instantáneas de la propagación del pulso en el Slinky en t =0.10, 0,17, 0,24, y 0,34 s. Los marcadores circulares indican las posiciones del centro de masa del Slinky. (C) Desplazamiento del centro de masa del Slinky, uCM, en función del tiempo. Los marcadores circulares corresponden a los puntos de tiempo considerados en (A) y (B). (D) Diagrama de desplazamiento espacio-temporal del pulso en propagación. (E) Señales de velocidad medidas en los bucles 10 y 80. (F) Evolución de la correlación cruzada de v10 (t) y v80 (t) en función de la amplitud de entrada Ain. El marcador triangular corresponde a Ain =100 mm. La línea punteada verde corresponde a la amplitud del solitón soportado, Como, predicho por las ecuaciones derivadas del estudio. Crédito de la foto:Bolei Deng, Universidad Harvard. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1166
A continuación, el equipo tiene la intención de dirigir el robot girando el último bucle en la parte posterior del dispositivo y controlando el ángulo de dirección. al tiempo que enfatiza la posibilidad existente de mover el robot a través de una amplia gama de superficies. Aunque Deng et al. solo usó un Slinky para realizar la locomoción impulsada por pulsos en este trabajo, los principios son generales y pueden expandirse a una amplia gama de sistemas extensibles a través de escalas para abrir avenidas para rastreadores a microescala adecuados para aplicaciones médicas.
© 2020 Science X Network