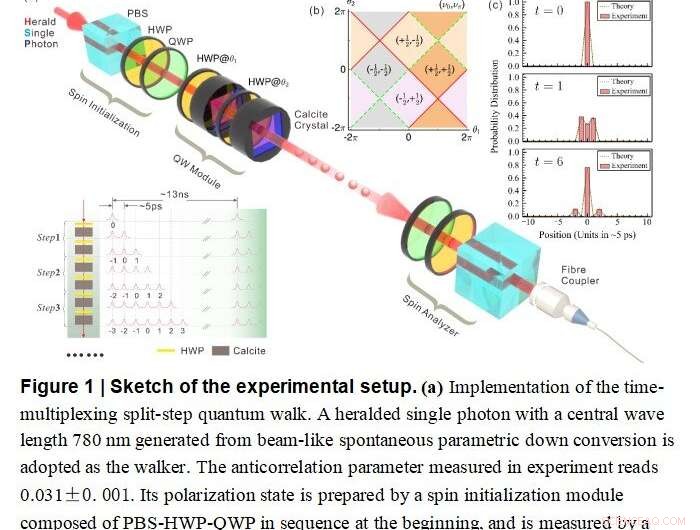
Bosquejo de la configuración experimental Crédito:por Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei-Wei Pan, Zhe Chen, Munsif Jan, Kai Sun, Jin-Shi Xu, Yong-Jian Han, Chuan-Feng Li, Guang-Can Guo
Los procesos dinámicos de desequilibrio son fundamentales en muchos contextos de tecnología cuántica. Sin embargo, ha sido un desafío clave identificar conceptos para su caracterización y clasificación, ya que los estados cuánticos resultantes desafían deliberadamente una descripción en términos de física estadística de equilibrio para realizar estados no accesibles por medios convencionales. Los científicos ahora han logrado una caracterización en términos de un parámetro de orden topológico dinámico para caminatas cuánticas, que representan una clase paradigmática de procesos de desequilibrio.
La coherencia en la dinámica cuántica está en el corazón de fenómenos fascinantes más allá del ámbito de la física clásica, como los efectos de interferencia cuántica, entrelazamiento de producción y fases geométricas.
Los procesos cuánticos de naturaleza dinámica inherente desafían una descripción en términos de un conjunto de física estadística de equilibrio. Hasta ahora, identificar los principios generales detrás de la dinámica cuántica unitaria subyacente que preserva la coherencia cuántica sigue siendo un desafío clave.
Los paseos cuánticos proporcionan una plataforma poderosa y flexible para realizar y sondear experimentalmente la evolución del tiempo cuántico coherente lejos del equilibrio térmico. A diferencia de los paseos al azar clásicos, Los paseos cuánticos se caracterizan por superposiciones cuánticas de amplitudes en lugar de distribuciones de probabilidad clásicas. Este genuino carácter cuántico ya se ha aprovechado en varios campos de la física, que van desde el diseño de algoritmos eficientes en el procesamiento de información cuántica, observación de dinámicas correlacionadas y localización de Anderson, a la realización de fenómenos físicos exóticos en el contexto de las fases topológicas.
Si bien el orden topológico se puede recuperar en el espacio real, El acceso a la información de amplitud compleja completa que caracteriza la superposición coherente sigue siendo uno de los desafíos clave en los experimentos de caminata cuántica.
En un nuevo artículo publicado en Ciencia y aplicación de la luz , Científicos del Laboratorio Clave de Información Cuántica de CAS y colaboradores internacionales informaron sobre la observación directa de un parámetro de orden topológico dinámico (DTOP) que proporciona una caracterización dinámica de los paseos cuánticos.
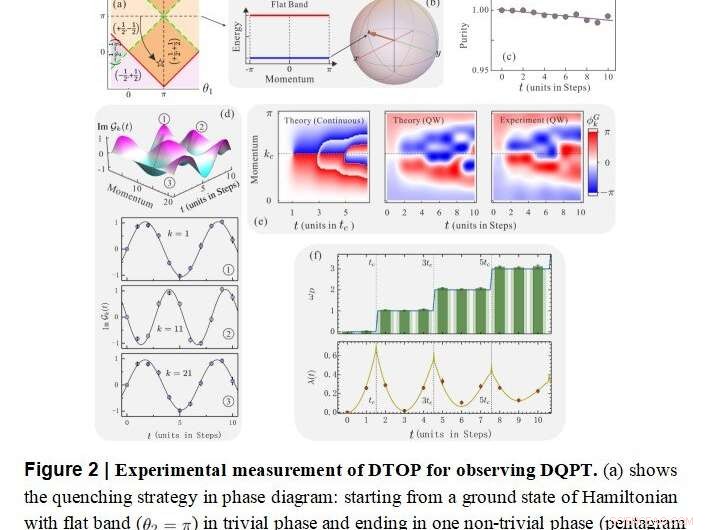
Medición experimental de DTOP para observar DQPT Crédito:por Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei-Wei Pan, Zhe Chen, Munsif Jan, Kai Sun, Jin-Shi Xu, Yong-Jian Han, Chuan-Feng Li, Guang-Can Guo
Para tal fin, realizaron una caminata cuántica de pasos divididos en un sistema fotónico utilizando el marco de multiplexación de tiempo. Usando una técnica desarrollada previamente, lograron una tomografía de estado completo del estado cuántico evolucionado en el tiempo durante hasta 10 pasos de tiempo completos. En tono rimbombante, esto proporcionó la información de amplitud compleja completa del estado de caminata cuántica.
"Esto es esencial para nuestro objetivo central de una clasificación dinámica del paseo cuántico utilizando el DTOP, dado que el DTOP mide el número de devanado de fase ω_D (t) en el espacio de momento, es decir, de la denominada fase geométrica de Pancharatnam (PGP) ".
De los resultados experimentales, encontraron que las transiciones dinámicas entre clases topológicamente distintas de paseos cuánticos se pueden distinguir de forma única por el comportamiento dependiente del tiempo observado de ω_D (t).
"Para una extinción entre dos sistemas con el mismo carácter topológico, encontramos ω_D (t) =0 para todos los pasos de tiempo; en lugar de, para una extinción entre dos sistemas topológicamente diferentes, ω_D (t) también comienza en ω_D (t =0) =0, pero cambia monótonamente su valor en ciertos momentos críticos, ", agregaron.
Generalizando estas observaciones, además establecieron una relación única entre el comportamiento de ω_D (t) y el cambio sobre un parámetro de extinción en las propiedades topológicas de un floquet hamiltoniano efectivo que describe estroboscópicamente el paseo cuántico.
Los científicos concluyen:"De esta manera, proporcionamos una perspectiva de desequilibrio sobre los paseos cuánticos, que puede entenderse como un punto de partida para abordar los procesos dependientes del tiempo desde un ángulo inherentemente dinámico que va más allá de la noción de física estadística del equilibrio. Con esto y el mapeo en extinciones en un sistema cuántico de muchos cuerpos equivalente, nuestro experimento ofrece una plataforma versátil para estudiar la dinámica coherente de no equilibrio de muchos modelos paradigmáticos como el modelo Su-Schrieffer-Heeger, la cadena de Kitaev de onda p, o el modelo Ising de campo transversal en el futuro ".