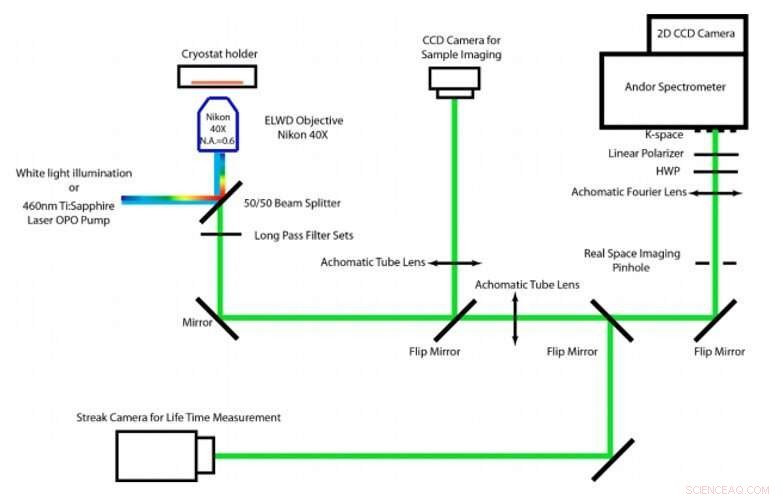
Esquema de la configuración casera para la caracterización láser, medición de la vida útil, y espectroscopía de fotoluminiscencia (PL) del espacio k dependiente de la polarización. Crédito:Actas de la Academia Nacional de Ciencias (PNAS), doi:https://doi.org/10.1073/pnas.1909948116
En física cuántica, Los excitones de Rydberg con alto valor principal pueden exhibir fuertes interacciones dipolo-dipolo. Sin embargo, polaritones (cuasipartículas) con un constituyente excitónico en un estado excitado, conocidos como polaritones de excitón de Rydberg (REP) aún no se han observado experimentalmente. En un estudio reciente ahora publicado en el Actas de la Academia Nacional de Ciencias de los Estados Unidos de América (PNAS) . Wei Bao y un equipo de investigación interdisciplinario en los departamentos de física, electrónica y el Centro de ciencia e ingeniería a nanoescala de la National Science Foundation (NSF) en los EE. UU., observó la formación de REP en un solo cristal CsPbBr 3 (bromuro de plomo y cesio) cavidad de perovskita; sin campos externos. Los investigadores notaron que los polaritones exhiben un fuerte comportamiento no lineal, que conducen a un condensado polariton coherente con un desplazamiento azul prominente. Los REP en CsPbBr 3 Las cavidades eran altamente anisotrópicas (mostrando diferentes propiedades en diferentes direcciones) con una gran proporción de extinción debido a la estructura cristalina ortorrómbica de la perovskita.
La coherencia cuántica solo es posible en presencia de interacciones fuertes entre polaritones de excitón debido a sus constituyentes excitónicos. Las observaciones de Bao et al. arroja luz sobre la importancia de la física de muchos cuerpos en sistemas de polaritones coherentes que involucran estados excitados de orden superior y allana el camino para explorar interacciones coherentes adicionales. Nuevas investigaciones beneficiarán a las tecnologías de procesamiento de información cuántica de estado sólido.
La electrodinámica cuántica de cavidades de estado sólido (CQED) puede ofrecer un control extraordinario de las interacciones de la materia luminosa dentro de una variedad de estructuras fotónicas. Aparte de simplemente modificar la densidad fotónica de los estados en el régimen de acoplamiento débil, CQED también puede facilitar la formación de nuevos cuasipartículas híbridas de materia ligera conocidas como polaritones de cavidad. Los polaritones de cavidad se crean en microcavidades semiconductoras (MC) debido al fuerte acoplamiento entre excitones y fotones, donde la tasa de acoplamiento puede ser más rápida que las tasas de disipación de los constituyentes. Las cuasipartículas bosónicas poseían una pequeña masa efectiva de su componente fotónico para heredar interacciones fuertes de su componente excitónico. Esta combinación permitió ricos fenómenos ópticos cuánticos como la condensación de polaritones, superfluidez y vórtices cuánticos:similares a los observados en los condensados de Bose-Einstein de átomos fríos (BEC), aunque a temperaturas más altas.
Las perovskitas de haluro de plomo emergentes con series de excitones de Rydberg son excelentes candidatas para investigar los estados excitón-polaritón y la condensación del polaritón para futuros circuitos fotónicos cuánticos. Los físicos habían demostrado recientemente de manera prometedora el láser de polaritón basado en el estado del excitón del suelo en un CsPbCl 3 microcavidad. En el presente trabajo, Bao y col. mostró la formación de polaritones de excitones híbridos en un monocristal de perovskita CsPbCl 3, incluidos los REP emergentes sin campos externos. En tono rimbombante, llegaron a la condensación de Bose-Einstein (un fenómeno cuántico exótico observado en gases atómicos diluidos) de polaritones con un desplazamiento azul prominente. Los polaritones eran anisotrópicos y los observados, El control preciso de la polarización era un requisito previo necesario en el procesamiento de información óptica cuántica. El trabajo supone un gran paso adelante en los sistemas fotónicos cuánticos de estado sólido y ofrece una plataforma única para nuevos pulsos cuánticos coherentes de muchos cuerpos. En paralelo, La investigación también abre una nueva puerta a las aplicaciones fotónicas cuánticas de estado sólido en la comunicación y la computación de la Internet cuántica.
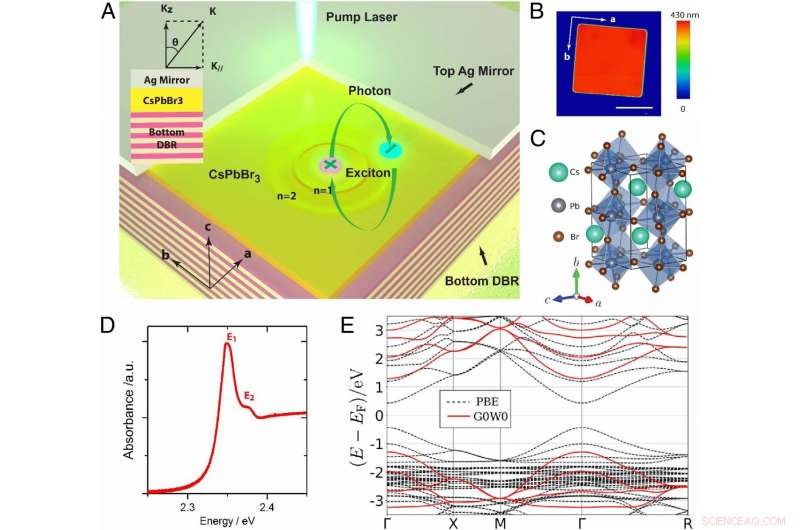
Esquemas de caracterización de materiales y dispositivos de microcavidad CsPbBr3. (A) La microcavidad CsPbBr3 está compuesta por un reflector Bragg distribuido en la parte inferior (DBR) de SiO2 / Ta2O5 de 16 pares, Microplacas de CsPbBr3 cultivadas por CVD con un espesor de 416 nm, y un espejo superior de Ag de 55 nm de espesor. También se indican los ejes de cristal. (B) Imagen de microscopía de fuerza atómica de la perovskita monocristalina de forma cuadrada uniforme CsPbBr3 usada en combinación con el espejo DBR inferior en los experimentos resumidos en la Fig. 2. Los ejes de cristal también están etiquetados. (Barra de escala:10 µm.) (C) La estructura cristalina estable calculada con DFT de CsPbBr3 ortorrómbica, con la etiqueta a, B, yc ejes cristalinos. Esta estructura da como resultado índices de refracción casi idénticos a lo largo de los ejes ayc, y un índice de refracción claramente diferente a lo largo del eje b. (D) El espectro de absorción no selectiva de polarización de la película monocristalina de CsPbBr3 en mica a 100 K. Se muestra claramente un pico de absorción del excitón E1 en el estado fundamental prominente junto con el estado E2 del excitón Rydberg n =2 excitado. (E) Estructuras de bandas PBE y G0W0 calculadas para CsPbBr3 ortorrómbico. Con la inclusión del acoplamiento espín-órbita, el intervalo de banda calculado por PBE se corrige a 2,5 eV por G0W0, coincidiendo bien con los experimentos. En tono rimbombante, a diferencia de GaAs, CsPbBr3 no tiene estados de banda cercanos o degenerados en los bordes de la banda de conducción o cenefa (punto Γ). Crédito:PNAS, doi:10.1073 / pnas.1909948116
El equipo de investigación seleccionó la perovskita de haluro metálico (CsPbCl 3 ) como anfitrión de excitones debido a su estabilidad química superior y eficiencia de emisión en comparación con las perovskitas de haluro orgánico-inorgánico. Para investigar las fuertes interacciones luz-materia en estos estados excitónicos, incorporaron el CsPbCl 3 microplaca en una cavidad plana de Fabry-Perot (componente fundamental de los interferómetros láser). Esta alta calidad de la cavidad ayudó a la formación de un REP debido a la interfaz nítida entre la perovskita y el espejo de metal en la configuración, junto con pérdidas reducidas por absorción de metales a temperaturas criogénicas.
Bao y col. observaron el acoplamiento coherente de estos estados y fotones de cavidad usando espectroscopía de espacio k después de enfriar las muestras a 90 K. Llevaron a cabo la caracterización del espacio k usando polarización lineal selectiva para mediciones de fotoluminiscencia (PL) y reflectividad. Midieron el PL con un láser de bomba no resonante de 460 nm y completaron las mediciones de reflectividad utilizando una fuente de luz blanca halógena de tungsteno no polarizada. El equipo obtuvo dos modos dispersivos tanto de PL como de mediciones de reflectividad, que identificaron como los estados polariton recién formados. La observación implicó un fuerte acoplamiento coherente entre la luz y un estado excitado por excitón, sin un campo externo para formar el REP esperado (Rydberg exciton polariton). Los polaritones mostraron una anisotropía de polarización extremadamente fuerte que se originó a partir de los índices de refracción de perovskita.
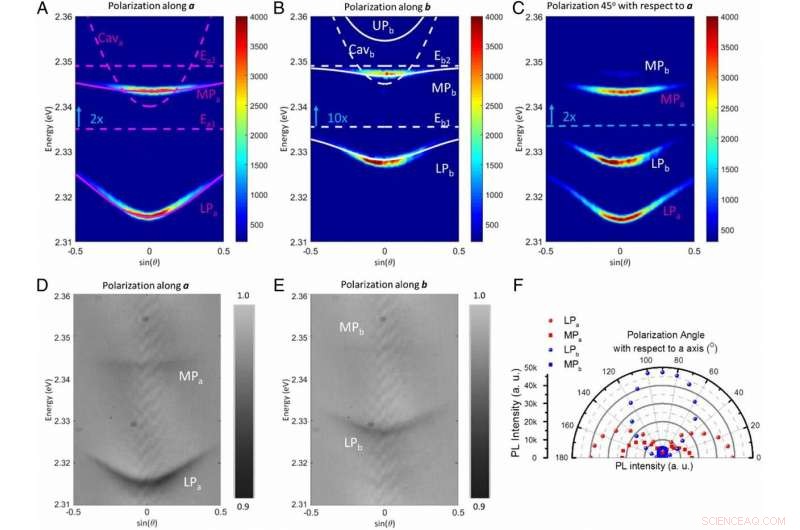
El PL con resolución de ángulo en el espacio k y la reflectividad de la luz blanca a 90 K. (B) a lo largo del eje del cristal b, y (C) 45 ° entre los ejes ay b. La intensidad del polariton PL de la rama media se magnifica 2 ×, 10 ×, y 2 × en A – C, respectivamente, debido a su débil emisión. El eje horizontal representa la función sinusoidal de los ángulos de inclinación de la luz de emisión θ con respecto al eje z, y el eje vertical es la energía de los fotones. El polaritón de la rama media MPa y MPb (mejor visto en C) se forman sin ambigüedades debido al estado de excitón n =2. La dispersión del polaritón se ajusta utilizando un modelo de oscilador acoplado. La energía del excitón y el modo de la cavidad fotónica (Cava y Cavb) antes del acoplamiento fuerte (línea discontinua) y la dispersión del polaritón ajustada (línea continua) se superponen con el mapa PL. Estos finos estados excitónicos y sus estructuras de polaritones solo pueden observarse a bajas temperaturas (<150 K). A temperaturas más altas, las muestras de la cavidad transitan desde una sola rama de polaritón inferior hasta un pico PL amplio (similar a la emisión de excitones desnudos). Los correspondientes mapas de reflectividad de luz blanca selectiva de polarización de la misma muestra (D) a lo largo del eje de cristal ay (E) a lo largo del eje de cristal b. La dispersión de los mapas de reflectividad del espacio k coincide muy bien con el ajuste de dispersión PL. (F) La dependencia de la polarización de la emisión de polaritones a un ángulo normal (θ =0 °). La tasa de extinción de estos 2 modos de emisión de rama inferior ortogonales es más de 50. Crédito:PNAS, doi:10.1073 / pnas.1909948116
Los investigadores definieron un condensado de polaritón (acoplamiento cuidadosamente diseñado entre la luz y la materia) como un conjunto coherente de una densidad finita de partículas en el estado de polaritón más bajo disponible. Describieron el estado utilizando un modelo de condensación disipativo de Bose-Einstein. Un condensado era posible a temperaturas superiores a las criogénicas debido a su pequeña masa efectiva (aproximadamente 10 4 masa de electrones) de las partículas híbridas de materia ligera y las fuertes interacciones entre ellas. A mayores densidades de portadores, las interacciones se volvieron significativas para generar un régimen no lineal estimulado para formar un estado de condensación cuántica macroscópicamente coherente.
Los científicos realizaron más análisis para confirmar la condensación de polaritones. Observaron tres regiones correspondientes; donde (1) las interacciones de polariton fueron insignificantes, (2) formaron interacciones estimuladas entre REP, y (3) formó el régimen de condensado. Los resultados justificaron la interpretación de Bao et al. formado en el estado estable de no equilibrio como un condensado de excitón-polaritón. En contraste con la condensación de polariton convencional, el equipo de investigación observó la participación de múltiples modos de polaritón debido a fuertes interacciones excitón-excitón en el estudio.
La fuerte interacción de los REP en la región no lineal también fue evidente en los cambios al azul de estas energías de polariton; el cambio no se produjo debido a un efecto de calentamiento a mayores potencias de la bomba láser. Cuando los investigadores extrajeron las posiciones de los picos de fotoluminiscencia en función de la potencia de la bomba, observaron modos de polaritón por debajo del umbral para mostrar cambios de azul notables debido a un pequeño efecto de desorden. Por encima del umbral, las interacciones repulsivas polariton-polariton se hicieron más prominentes, provocando que los modos REP muestren fuertes cambios en azul. El estudio demostró interacciones de polariton muy fuertes con la participación de estados excitónicos de Rydberg.
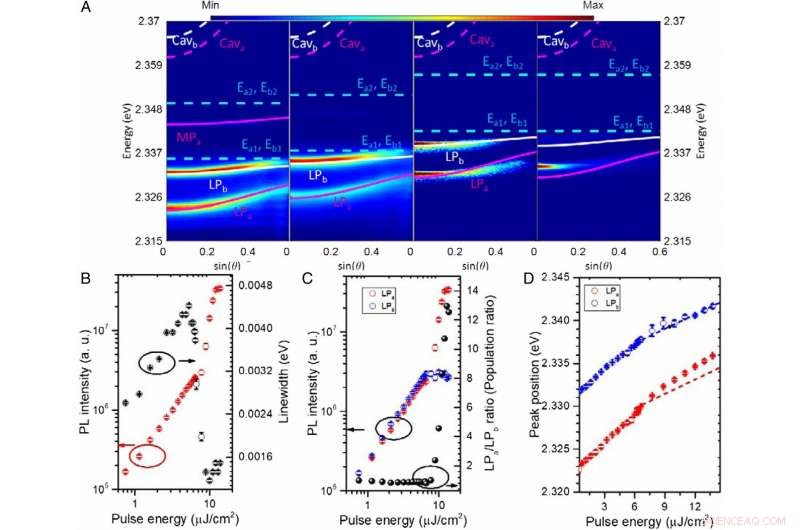
Comportamiento anómalo del condensado de excitón-polaritón a 55 K. (A) El mapa PL resuelto del ángulo dependiente de la potencia del espacio k tomado en 0.05 Pth, 0.4Pth, Pth, y 1.4Pth (de izquierda a derecha). La excitación es luz de 460 nm polarizada a lo largo de la diagonal a – b. La muestra es un poco más delgada y más desafinada que en la Fig. 2. Los 2 conjuntos de modos ortogonales de excitón-polaritón de Rydberg se identifican de manera inequívoca y las dispersiones de polaritón se ajustan utilizando el mismo modelo de oscilador acoplado que antes. La energía de excitón desacoplada y la dispersión del modo de cavidad fotónica (línea discontinua) y el ajuste de dispersión de polaritón (línea continua) se superponen con el mapa PL. El color magenta representa el modo de polarización a lo largo de un eje, mientras que el color blanco representa el modo de polarización ortogonal a lo largo del eje b (Fig. 1 A y C). El panel 1.4Pth muestra el mismo ajuste que en Pth para enfatizar el cambio de azul por encima del umbral. La pequeña desviación en el ajuste de ángulo alto (senθ) de la rama de polaritón LPa y LPb en Pth y 1.4Pth se debe a la renormalización del modo de cavidad en el umbral. El condensado de polaritón experimenta un proceso de condensación anómalo en el que el LPb muestra un aumento más rápido que el estado LPa de menor energía entre el segundo y el tercer panel. Esto se debe a una interacción de excitones más fuerte a lo largo del eje b. A medida que la densidad de la bomba se acerca a la densidad de condensación, el LPa finalmente experimenta un aumento superlineal con dispersión estimulada al estado más bajo de LPa, mientras que LPb no muestra más aumento. (B) Gráfico log-log de la intensidad PL integrada del modo LPa a θ =0 ° y el ancho completo a la mitad del máximo (FWHM) del modo LPa a θ =0 ° frente a la potencia de la bomba. Se observa no linealidad y estrechamiento del ancho de línea del modo de polaritón cuando la intensidad de excitación excede el umbral de condensación. Las barras de error de ajuste del procesamiento de datos se muestran en B – D. (C) Gráfico log-log del modo LPa (punto rojo) y del modo LPb (punto azul) en θ =0 °. Intensidad PL y relación de los 2 modos frente a la potencia de la bomba. (D) Posición pico de PL tanto del modo LPa (punto rojo) como del modo LPb (punto azul) a θ =0 ° en función de la potencia de la bomba. Se observa un fuerte cambio al azul de los modos de polaritón por debajo del umbral debido a las fuertes interacciones de los excitones y al desorden potencial del sistema (39). Después del umbral de condensación, un cambio de azul prominente en los modos LPa y LPb es el resultado de la interacción polaritón-polaritón y la interacción polaritón-depósito. La teoría predice el desplazamiento azul contribuido por la interacción 1s-polaritón resultante del excitón se traza en la línea roja y azul punto-punto-guión como guía. El valor observado experimental es mayor que la estimación de la interacción pura 1s-excitón. Crédito:PNAS, doi:10.1073 / pnas.1909948116
Está más allá del alcance del presente trabajo establecer una teoría más detallada para calibrar con precisión la densidad de polaritones, junto con el análisis cuantitativo de las interacciones dipolo-dipolo y las interacciones entre excitones para obtener una mejor estimación de la fuerza de la interacción. Sin embargo, Las presentes observaciones experimentales de REP con interacciones mejoradas prometen una mayor exploración de las interacciones de Rydberg en sistemas de estado sólido en el futuro.
De este modo, Wei Bao y sus colegas descubrieron sorprendentemente REP en una cavidad de perovskita de cristal único, proporcionándoles un control coherente de los estados cuánticos finos observados. La fuerte interacción intrínseca del excitón y la birrefringencia óptica en la perovskita conducen a la observación de la dinámica de condensación de polaritón. Este resultado prometía un estado macroscópicamente coherente robusto para aplicaciones cuánticas. El descubrimiento presenta una plataforma única para estudiar la física cuántica coherente de muchos cuerpos para permitir la manipulación sin precedentes de estos estados de Rydberg dentro de las aplicaciones cuánticas. Bao y col. tienen como objetivo explorar los nuevos estados a través de la ingeniería de composición química, control de fase estructural y campos de calibre externos. Los científicos demostraron que controlar el REP y sus condensados agrega nuevos sabores para estudiar el láser de polaritón, superfluidez y vórtices. En tono rimbombante, el trabajo tiene un gran potencial para aplicaciones en comunicación cuántica y estimulación cuántica.
© 2019 Science X Network