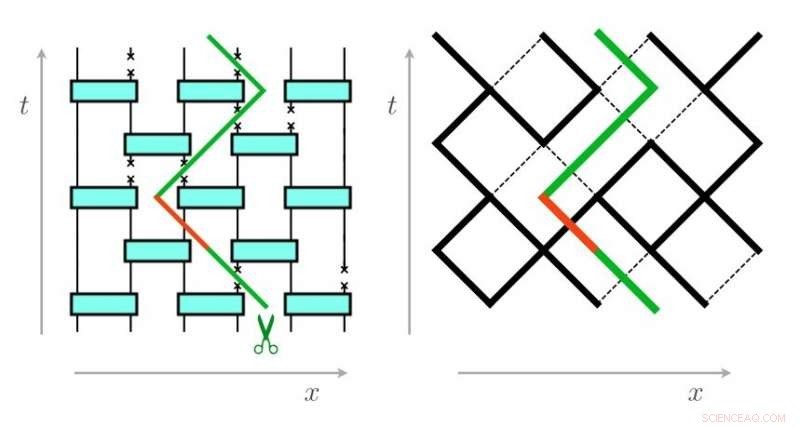
En el problema de corte mínimo, el objetivo es abrir un camino a través de una red rompiendo la menor cantidad de enlaces (aquí, solo es necesario romper el vínculo rojo). El problema es idéntico para un circuito eléctrico (izquierda) y una red (derecha) que representa un sistema cuántico entrelazado. Crédito:Skinner, et al. © 2019 Sociedad Estadounidense de Física
Muchos experimentos famosos han demostrado que el simple hecho de observar un sistema cuántico puede cambiar las propiedades del sistema. Este fenómeno, llamado "efecto observador, "aparece, por ejemplo, cuando el gato de Schrödinger se vuelve vivo o muerto (pero ya no ambos) después de que alguien se asoma en su caja. La observación destruye la superposición del estado del gato, o en otras palabras, colapsa la función de onda que describe las probabilidades de que el gato se encuentre en cada uno de los dos estados.
En un nuevo periódico Los físicos han investigado más a fondo exactamente cómo las mediciones afectan el entrelazamiento cuántico, que en este contexto es equivalente a la medida en que un sistema está en superposición. Estudios anteriores han demostrado que, cuando se deja que un sistema cuántico evolucione sin interferencias externas, su grado de enredo tiende a aumentar. Es decir, Los sistemas cuánticos tienden a derivar con el tiempo hacia estados con un alto grado de superposición cuántica.
Por otra parte, realizar una medición en un estado entrelazado tiende a disminuir su entrelazamiento. Esto sucede porque una medición en un estado de giro (por ejemplo) colapsa y gira a un estado definido, lo que hace que ese giro se desenrede de los otros giros, cuyos estados permanecen en superposición. Esto reduce la cantidad de enredos en el sistema en general.
En el nuevo periódico, Los físicos han demostrado a través de simulaciones por computadora y argumentos teóricos que, cuando las mediciones se realizan a una velocidad que excede un valor crítico, se produce una transición de fase inducida por la medición. Esto hace que el sistema pase bruscamente de una fase de "entrelazamiento", en el que la cantidad de enredos crece continuamente con el tiempo, a una fase de "desenredado", en el que todavía existe algún enredo, pero su tasa de crecimiento cae a cero.
Los físicos Brian Skinner en MIT, Jonathan Ruhman en el MIT y la Universidad Bar-Ilan, y Adam Nahum en la Universidad de Oxford, han publicado su artículo sobre la transición de fase para el entrelazamiento en un número reciente de Revisión física X .
"Uno de los grandes éxitos de la física es su capacidad para describir las transiciones de fase:el cambio brusco de las propiedades de los materiales cuando se varía algún parámetro externo, como el agua que de repente se congela en hielo cuando cae por debajo de los 32 grados Fahrenheit, "Skinner dijo Phys.org . "Lo que hemos demostrado es que este mismo lenguaje se puede aplicar a un proceso dinámico que implica entrelazamiento cuántico. Es decir, las propiedades dinámicas del crecimiento por entrelazamiento también tienen una transición de fase en función de un parámetro externo, que es la velocidad a la que ocurren las mediciones. Para nosotros, esta es una hermosa y sorprendente conexión! "
Los investigadores desarrollaron un modelo de esta transición de fase inducida por la medición basado en un famoso problema de la teoría de la filtración llamado "rejilla de resistencias vandalizadas". En este problema, un vándalo intenta encontrar el menor número de enlaces (llamado "camino más corto" o "corte mínimo") para cortar una red eléctrica para desconectar completamente la red. Los investigadores demostraron que el problema de calcular la entropía del entrelazamiento en un sistema cuántico es equivalente a este problema de optimización, en el que el objetivo es encontrar un corte mínimo a través de una red desordenada que separa la red en dos partes.
En un sistema enredado, la red representa el sistema cuántico, y cada medida representa romper uno de los enlaces. El grado de enredo en el sistema está determinado por el tamaño del corte mínimo en esta red, es decir., el número total de enlaces continuos que deben romperse para separar el sistema del resto de la red. En un sentido, este número indica la frecuencia con la que se pueden realizar las mediciones antes de que un sistema entrelazado pase a la fase desenredada. Como las diferentes redes tienen diferentes números y arreglos de enlaces, la tasa de medición crítica difiere para diferentes sistemas.
Los físicos esperan que la comprensión de esta transición de fase inducida por la medición en la dinámica de entrelazamiento pueda tener implicaciones útiles para el desarrollo de simulaciones de sistemas cuánticos. El entrelazamiento juega un papel importante en la determinación de la dificultad de simular la dinámica cuántica en una computadora clásica. Como resultado, la transición de fase entrelazada a desenredada implica la existencia de una transición de fácil a difícil para las simulaciones. Esto puede permitir a los investigadores predecir mejor la dificultad de las simulaciones y buscar alternativas más sencillas.
“Nuestro hallazgo tiene una implicación inmediata para la cuestión de qué tan difícil es simular sistemas cuánticos usando computadoras clásicas, ", Dijo Skinner." También puede ser importante para los esquemas de computación cuántica, que a menudo se basan en mantener un enredo de largo alcance ".
En el futuro, los investigadores planean investigar cuán universal es su modelo.
"Hay diferentes formas de describir matemáticamente el entrelazamiento cuántico, "Dijo Skinner." Lo que mostramos fue que una de estas descripciones es perfectamente análoga a un problema de percolación clásico. Pero en este momento no está claro qué tan genérica es esta analogía, y si otras formas de describir el entrelazamiento pertenecen a la misma "clase de universalidad". La primera prioridad en este momento es establecer si la analogía es solo una aproximación que funciona en algunas situaciones artificiales, o si es completamente genérico en una amplia gama de descripciones y configuraciones experimentales ".
Vea las publicaciones de Twitter del Dr. Skinner en el periódico.
© 2019 Science X Network