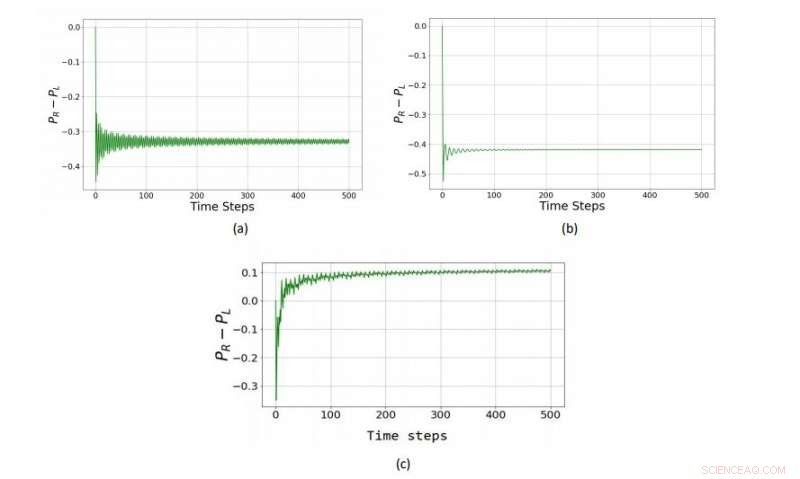
En una versión cuántica del juego de Parrondo jugado con una moneda de tres estados (un qutrit), las dos estrategias perdedoras (a) y (b) se combinan en una estrategia ganadora (c). Crédito:Rajendran et al. © 2018 EPL
Los físicos han demostrado que la paradoja de Parrondo, una aparente paradoja en la que dos estrategias perdedoras se combinan para hacer una estrategia ganadora, puede surgir como un juego de monedas con una sola moneda en el reino cuántico. pero solo cuando la moneda tiene tres estados (cara, cruz, y un lado) en lugar de los dos convencionales.
En general, La paradoja de Parrondo, también llamado juego de Parrondo, solo funciona cuando las dos estrategias perdedoras dependen de alguna manera entre sí y se combinan de tal manera que cambian las condiciones que las llevan a perder. Desde que fue descubierto por el físico Juan Parrondo en 1996, La paradoja de Parrondo ha encontrado aplicaciones en ingeniería, Finanzas, y biología evolutiva, entre otras áreas.
Una de las formas más sencillas de implementar un juego de Parrondo se describe en esta entrada de Wikipedia. Suponga que tiene $ 100, y puedes elegir jugar cualquier combinación de dos juegos. En el primer juego, pierde $ 1 cada vez que juega. En el segundo juego, ganas $ 3 si te quedan una cantidad par de dólares, y pierde $ 5 si le queda un número impar de dólares. Si solo juega el primer juego o solo juega el segundo juego, eventualmente perderás todo tu dinero, por lo que jugar cada juego por sí solo es una estrategia perdedora. Sin embargo, si alterna entre los dos juegos, comenzando con el segundo juego, entonces ganarás $ 2 por cada dos juegos que juegues, para que las dos estrategias perdedoras puedan combinarse en una estrategia ganadora.
En el nuevo estudio, los físicos Jishnu Rajendran y Colin Benjamin del Instituto Nacional de Educación e Investigación Científica, HBNI, En India, han demostrado un juego de Parrondo usando una moneda de tres estados, que representan con un qutrit, un sistema cuántico con tres estados.
"Los juegos de Parrondo se han visto en un contexto clásico, "Benjamín dijo Phys.org . "Nuestro objetivo en este trabajo era mostrar cómo implementarlo en un contexto cuántico, en particular en un paseo cuántico. Desafortunadamente, la versión cuántica de este juego cuando se implementó con una sola moneda (qubit) en un paseo cuántico falló en los límites asintóticos. Lo que mostramos en este trabajo es que un qutrit puede implementar este juego de Parrondo en una caminata cuántica ".
En el paseo cuántico un jugador comienza en el origen y se mueve hacia la derecha (dirección positiva) o hacia la izquierda (dirección negativa) según el resultado de un lanzamiento de moneda. Si cabezas, el jugador se mueve a la derecha; si colas, izquierda; y si el resultado es "lateral, "entonces el jugador interpreta eso como un" estado de espera "y permanece en el mismo lugar. Como el qutrit es un sistema cuántico, también puede estar en una superposición de estos estados, en cuyo caso el jugador se mueve a la posición correspondiente, en algún lugar entre un paso completo hacia la izquierda o hacia la derecha. Al final del juego, si la probabilidad de que el jugador se encuentre a la derecha del origen es mayor que la probabilidad de que se encuentre a la izquierda del origen, el jugador gana. De lo contrario, ellos pierden.
Usando algunos de los métodos estándar en física de partículas para definir los conceptos de un lanzamiento de moneda y reglas de juego con una superposición de estados, los físicos demostraron varios ejemplos de juegos que resultan en pérdidas cuando se juegan individualmente, pero cuando se combinan en una secuencia alterna dan como resultado un resultado ganador. También demostraron ejemplos de lo contrario. Por ejemplo, Dos juegos que resultan en una victoria y un empate cuando se juegan individualmente pueden resultar en un resultado perdedor cuando se combinan.
Los físicos también demostraron que, aunque no es posible implementar un juego de Parrondo usando una sola moneda de dos caras (qubit), es posible implementar un juego de Parrondo usando dos monedas de dos caras (dos qubits). Los estados adicionales esencialmente brindan flexibilidad adicional con la que combinar estrategias que pueden superar las condiciones de pérdida.
Dadas las amplias aplicaciones de los juegos clásicos de Parrondo, los físicos esperan que la versión cuántica pueda conducir a nuevos conocimientos sobre el diseño de algoritmos cuánticos.
"El juego de Parrondo es una receta para demostrar que no siempre es necesario buscar una estrategia (o algoritmo) ganadora en un juego, "Benjamin dijo." Clásicamente, hay muchas aplicaciones de los juegos de Parrondo, que van desde la explicación de los procesos fisiológicos en la célula hasta el aumento de nuestra comprensión de los motores brownianos e incluso la inversión de cartera diversificada. Clásicamente Se ha demostrado que la paradoja de Parrondo funciona utilizando paseos aleatorios clásicos.
"La implementación de un juego de Parrondo en una caminata cuántica tendría implicaciones para diseñar algoritmos cuánticos mejores o más rápidos. Un algoritmo que utiliza principios cuánticos como la superposición y / o el entrelazamiento es un algoritmo cuántico. Un algoritmo, si se puede implementar en una caminata cuántica, sería más lucrativo que uno que solo se puede implementar en una caminata aleatoria clásica. A medida que los paseos cuánticos se extienden cuadráticamente más rápido que los paseos aleatorios clásicos, un algoritmo implementado en una caminata cuántica tardará mucho menos en completarse que uno en una caminata aleatoria clásica. Más lejos, la implementación exitosa del juego de Parrondo en una caminata cuántica proporciona una explicación algorítmica para los trinquetes cuánticos [sistemas que tienen movimiento en una sola dirección] ".
© 2018 Phys.org