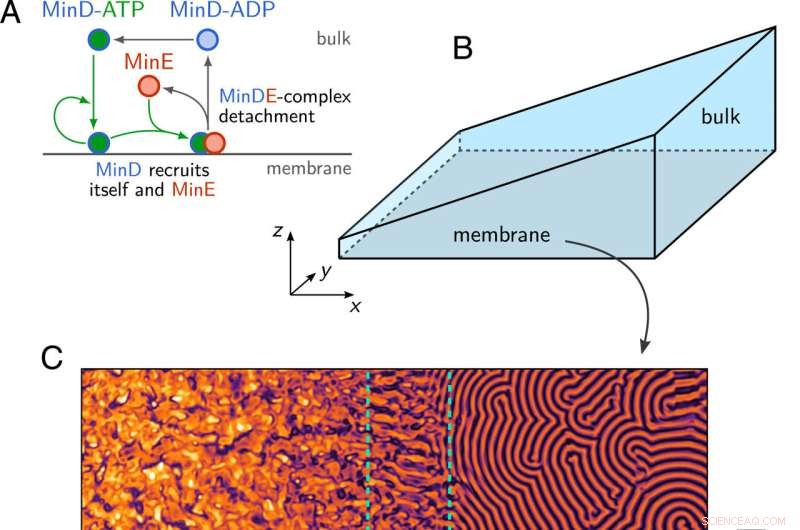
(A) Ilustración esquemática de la red de reacción de la proteína Min. (B) Geometría de cuña con una superficie de membrana en el plano inferior (z =0) y altura aparente H(x) que aumenta linealmente a lo largo de la dirección x. (C) Instantánea de la densidad de la membrana de MinD, obtenida mediante la simulación numérica de las ecuaciones dinámicas de Min. 1–3 en la geometría que se muestra en B. Se observan regiones con patrones caóticos, ondas estacionarias (SW, contorno verde discontinuo) y ondas viajeras (TW) a lo largo de la membrana y en diferentes alturas aparentes. Crédito:Actas de la Academia Nacional de Ciencias (2022). DOI:10.1073/pnas.2206888119
Para muchos procesos importantes para la vida, como la división celular, la migración celular y el desarrollo de órganos, la formación espacial y temporal correcta de patrones biológicos es esencial. Para comprender estos procesos, la tarea principal no consiste en explicar cómo se forman los patrones a partir de una condición inicial homogénea, sino en explicar cómo los patrones simples se transforman en otros cada vez más complejos. Iluminar los mecanismos de esta autoorganización compleja en varias escalas espaciales y temporales es un desafío clave para la ciencia.
Las llamadas técnicas de "grano grueso" permiten simplificar tales sistemas multiescala, de modo que pueden describirse con un modelo reducido a escalas de tiempo y longitud grandes. "Sin embargo, el precio que paga por la granularidad gruesa es que se pierde información importante sobre los patrones a pequeña escala, como el tipo de patrón. Pero la cuestión es que estos patrones juegan un papel decisivo en los sistemas biológicos. Para dar un ejemplo , controlan procesos celulares importantes", explica Laeschkir Würthner, miembro del equipo dirigido por el profesor Erwin Frey, físico de LMU, y autor principal de un nuevo estudio publicado en Proceedings of the National Academy of Sciences. que supera este problema.
En colaboración con el grupo de investigación del Prof. Cees Dekker (TU Delft), el equipo de Frey ha desarrollado un nuevo enfoque de grano grueso para los llamados sistemas de reacción-difusión de conservación de masa, en el que el análisis a gran escala de las densidades totales de las partículas involucradas permiten la predicción de patrones a pequeña escala.
Los científicos ilustraron el potencial de su enfoque con el sistema de proteínas Min, un modelo paradigmático para la formación de patrones biológicos. La bacteria E. coli utiliza varias proteínas Min que circulan en una célula para determinar en qué lugar tiene lugar la división celular. Un factor decisivo aquí es que las proteínas involucradas ocurren en diferentes frecuencias según su ubicación en la célula y su estado químico, es decir, tienen una variedad de densidades diferentes.
"Ahora hemos logrado reducir la complejidad de este sistema mediante el desarrollo de una teoría que se basa únicamente en las densidades totales de las proteínas, de modo que podemos reflejar completamente la dinámica de formación de patrones", dice Frey. "Esta es una gran reducción. Los cálculos numéricos ahora se realizan en cuestión de minutos en lugar de meses".
Los investigadores pudieron confirmar experimentalmente las predicciones teóricas del modelo, según las cuales la distribución de las proteínas depende de la geometría del entorno. Hicieron esto reconstruyendo el sistema de proteína Min en una celda de flujo in vitro, y los resultados mostraron los mismos patrones de proteína que se revelaron en la simulación.
"Tal reconstrucción de información en una pequeña escala de longitud a partir de una dinámica reducida a nivel macroscópico abre nuevos caminos para una mejor comprensión de los sistemas complejos de múltiples escalas, que ocurren en una amplia gama de sistemas físicos", dice Frey. Los sistemas de formación de patrones biológicos se caracterizan mejor a través de la geometría que de las simulaciones