
En este ejemplo, una esquina del triángulo está frustrada. Crédito:Johan Jarnestad / La Real Academia Sueca de Ciencias, CC BY-NC
El Premio Nobel de Física para 2021 ha sido otorgado conjuntamente al italiano Giorgio Parisi, Syukuro Manabe de Japón y Klaus Hasselmann de Alemania por sus "contribuciones innovadoras a nuestra comprensión de los sistemas complejos".
Cuando escuché la noticia Apenas podía creerlo. Estudié para mi tesis de maestría y mi doctorado. en física teórica con el profesor Parisi en la Universidad Sapienza de Roma.
Cuando digo que estaba incrédulo no me malinterpretes. De todas las personas que he conocido en mi experiencia de investigación, tal vez en mi vida, él es sin duda el más ingenioso. Así que no me sorprendió la decisión del comité del Premio Nobel de nombrarlo Laureado. Bastante, Fue su decisión de reconocer sus "contribuciones a nuestra comprensión de los sistemas complejos" lo que despertó mi interés.
Este premio para el profesor Parisi, dividido con meteorólogos pioneros, el profesor Manabe y el profesor Hasselmann, es un reconocimiento asombroso de todo un área de investigación, tal vez un poco menos glamorosa que la relatividad general o la teoría de cuerdas, que intenta comprender y modelar lo que en física llamamos "sistemas complejos".
Estos incluyen cosas como ecosistemas climáticos, sistemas financieros, y fenómenos biológicos, para nombrar unos pocos. La gran variedad de sistemas complejos —representados en mercados fluctuantes y estorninos en bandada— hace que sea muy difícil derivar algún tipo de reglas universales para ellos. El trabajo de Parisi nos ha permitido derivar conclusiones sin precedentes sobre tales sistemas que, en la superficie, mira al azar, impredecible e imposible de modelar teóricamente.
A diferencia de otros modelos de física, los sistemas complejos no son una colección de partículas idénticas, interactuar regularmente de una manera consistente y predecible. En lugar de, los sistemas complejos son sistemas de elementos, potencialmente diferentes entre sí, interactuar de formas diferentes y aparentemente impredecibles mientras se expone a diversas condiciones externas.
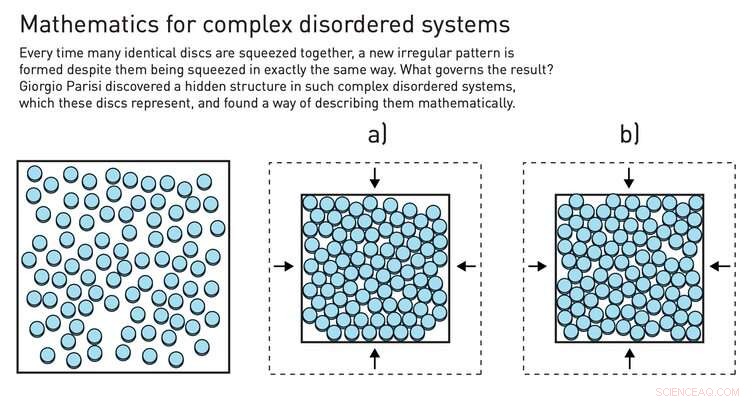
El truco de la réplica se puede realizar comprimiendo bolas en una caja. Crédito:Johan Jarnestad / La Real Academia Sueca de Ciencias, CC BY-NC
Un trampolín para modelar sistemas complejos es la teoría de los "sistemas desordenados". Estos son esencialmente sistemas en los que diferentes pares de elementos experimentan diferentes, fuerzas potencialmente conflictivas que pueden llevar a los elementos a "frustrarse".
Una forma de ilustrar esto es imaginar un partido (un sistema social cerrado), donde Alice puede querer charlar con Bob, y Bob puede querer charlar con Charlie, pero es posible que Charlie no quiera charlar con Alice. Aquí hay frustración, entonces, ¿qué deberían hacer?
La investigación del profesor Parisi aclaró lo que sucede cuando la frustración ocurre en sistemas desordenados y complejos. Identificó que los sistemas complejos son capaces de recordar sus trayectorias a lo largo del tiempo, y puede quedarse atascado en estados subóptimos durante mucho tiempo.
En nuestro ejemplo de fiesta, imagina a Alicia, Beto, Charlie y otros invitados que cambian de forma irregular los grupos de conversación y los socios, con la esperanza de encontrar el mejor grupo de personas para chatear, pero potencialmente nunca encontrarlo. Ese es el estado subóptimo en el que los sistemas complejos pueden atascarse.
Patrones del desorden
Una de las muchas herramientas teóricas que el profesor Parisi ha utilizado para establecer su teoría es el llamado "truco de la réplica", un método matemático que toma un sistema desordenado, lo replica varias veces, y compara cómo se comportan las diferentes réplicas del sistema. Puedes hacerlo, por ejemplo, comprimiendo canicas en una caja, que formará una configuración diferente cada vez que realice la compresión. A lo largo de muchas repeticiones, Parisi sabía pueden surgir patrones reveladores.
Este método es ahora uno de los pocos pilares teóricos para el desarrollo de toda la teoría de sistemas complejos tal como la conocemos hoy. Se ha demostrado que la teoría del profesor Parisi ofrece predicciones fiables sobre las propiedades estadísticas de sistemas complejos que van desde líquidos superenfriados (líquidos por debajo de su temperatura de solidificación), líquidos congelados, sólidos amorfos como el vidrio, e incluso bandadas de estorninos.
La teoría de los sistemas desordenados nos permite dar sentido a la hermosa aparición de patrones de vuelo coherentes dentro de bandadas reducidas de aves, que logran mantenerse juntas y formar grandes agrupaciones a pesar de las condiciones adversas.
El mismo marco se ha utilizado para dar sentido al clima de la Tierra. Los meteorólogos que comparten el premio Nobel con el profesor Parisi habrán confiado en los avances de la física teórica para producir los modelos que usamos ahora para demostrar de manera confiable el calentamiento global.
Tuve la oportunidad de discutir estos temas con el profesor Parisi en Roma, mientras se llevaban a cabo sus experimentos con bandadas de pájaros y durante sus simulaciones por ordenador sobre el comportamiento del vidrio. Sabiendo un poco de su mente No me sorprende en absoluto que haya sido galardonado con el premio Nobel de física.
Pero me sorprende gratamente que el campo de los sistemas complejos, que está empujando silenciosamente la frontera de la investigación teórica en física, se le ha dado esta exposición. Este premio Nobel ha otorgado nueva legitimidad y, podemos esperar nuevas mentes, a esta fascinante área de la física contemporánea.
Este artículo se ha vuelto a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 