
Crédito:Universidad de Connecticut
Quien dijo que las reglas estaban hechas para romperse no era un físico. Cuando algo no actúa de la manera que crees que debería, o las reglas están mal, o hay nueva física por descubrir. Que es exactamente lo que Connor Occhialini de UConn, un estudiante de último año con honores con especialización en física y matemáticas, encontrado cuando comenzó a investigar el fluoruro de escandio.
El fluoruro de escandio es un cristal transparente con forma cúbica, un subproducto de la minería. No se usa comercialmente y no sería particularmente interesante para nadie excepto por una cosa extraña:se encoge a medida que se calienta.
La mayoría de los materiales se hinchan a medida que se calientan. Los materiales realmente simples como el gas hidrógeno se hinchan porque el calor hace que sus átomos se muevan más rápido, chocando más entre sí, por lo que el mismo número de átomos de hidrógeno necesita más espacio. Los materiales más complicados también se hinchan, razón por la cual su puerta de entrada de madera tiende a quedarse pegada en verano. Pero los sólidos como la madera no pueden hincharse tanto como un gas porque sus átomos están estrechamente unidos entre sí en largos, moléculas entrelazadas, así que simplemente se mueven, hinchando un poco la puerta.
El fluoruro de escandio debe estar haciendo otra cosa, razonó Occhialini. Su asesor para su proyecto de física de honores, Jason Hancock, había estado trabajando con fluoruro de escandio, y le pidió a Occhialini que estudiara un modelo de la dinámica del cristal. El fluoruro de escandio tiene una estructura bastante simple:es un cristal sólido, con cada átomo de escandio rodeado por seis flúor para hacer pilas de octaedros (diamantes de ocho caras). Los investigadores esperaban que la estructura simple fuera fácil de entender. Entendiendo la extraña 'expansión térmica negativa del fluoruro de escandio, 'como los físicos llaman la contracción relacionada con el calor, podría dar una visión más general de otros, materiales más complejos que hacen lo mismo.

Figura 1. Ayuda, ¡Me estoy encogiendo! Los diamantes negros representan moléculas de fluoruro de escandio. Mientras se calientan ellos giran, y los contratos de cristal. Observe cómo las moléculas cercanas al centro de masa (punto central) se mueven menos que las moléculas más cercanas al borde del cristal. Crédito:Universidad de Connecticut
El primer paso de Occhialini fue simplificar el problema. Entonces, en lugar de un cristal tridimensional, decidió pensar en ello como una hoja bidimensional.
Cada diamante negro representa una molécula de fluoruro de escandio. Los átomos de escandio (puntos azules) están en el centro de cada diamante, y un átomo de flúor está en cada esquina.
La mayor parte del tiempo los enlaces entre átomos son flexibles. Entonces, en un sólido cristalino normal, el fluoruro de calcio, por ejemplo, los átomos de flúor y calcio podrían moverse de forma independiente cuando el material se calentara. Mientras se movían ocuparían un poco más de espacio, y el sólido se hincharía. Comportamiento sólido normal.
Pero Occhialini se preguntó si tal vez eso no era lo que estaba sucediendo con el fluoruro de escandio. Quizás en este modelo, ¿Debería asumir que los enlaces que conectan cada flúor con su escandio eran rígidos? Tan rígidos que los enlaces flúor-escandio no se mueven en absoluto, por lo que los diamantes son como bloques sólidos. Los únicos lugares donde la estructura podría flexionarse cuando se calentara serían los átomos de flúor, que actuarían como pequeñas articulaciones. Mientras el cristal se calentaba, los pequeños bloques de fluoruro de escandio se inclinarían alrededor de los fluoruros en las esquinas. Eso es lo que ves sucediendo en la imagen. Notarás que cuando los diamantes se inclinan, toda la estructura se hace más pequeña. De hecho, se aprieta. El contorno azul muestra la estructura en su punto más frío, estado perfectamente ordenado, sin movimiento molecular. Cuando los diamantes se inclinan ocupan un volumen total menor que el delineado por el contorno azul. Esta es una expansión térmica negativa.
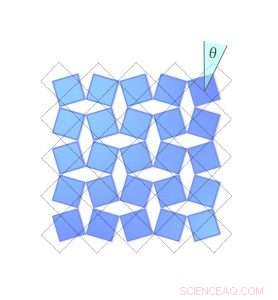
Figura 2. Cuánto se contrae un cristal de fluoruro de escandio depende de cuánto giran las moléculas. Aquí, el diamante azul en la esquina superior derecha gira en el sentido de las agujas del reloj, barriendo un ángulo theta. Las líneas de puntos muestran su posición cuando el ángulo era cero. Crédito:Universidad de Connecticut
Occhialini descubrió que se puede describir matemáticamente esta contracción, usando solo el ángulo de inclinación de las moléculas. Llamó al ángulo Θ (theta). Cuando los bloques de fluoruro de escandio se inclinan en un ángulo Θ, la distancia entre el centro de cada bloque se acorta en un factor de coseno Θ, y el volumen total del cristal se contrae.
Para calcular esa contracción (o, en un material normal, expansión) en detalle, Occhialini agregó un tercer término a la ecuación clásica que describe la energía de un cristal vibrante. Los dos primeros términos de la ecuación estándar describen la energía potencial que tiene un cristal de la flexión en cada unión molecular, más la energía cinética de rotación de cada molécula. La ecuación de Occhialini también describe la energía cinética de traslación de las moléculas, no solo por girar, pero también acercándose y alejándose de sus posiciones originales a medida que giran. Cuanto más lejos estén del centro de masa del cristal, cuanto más se mueven. Vuelva a mirar la Figura 1 y observe el punto en el medio; ese es el centro de masa. Los diamantes en el medio apenas se mueven en relación con él, mientras que los diamantes de los bordes se mueven mucho. Ahora imagina cuánta diferencia habría si el cristal tuviera millones de moléculas en lugar de solo 25. Y ahora comprendes lo importante que podría ser ese tercer término para la energía del cristal.
Ahora, moléculas siendo moléculas, no solo se encogen y se quedan ahí. Se mueven constantemente y cuanto más calientes se ponen, cuanto más se mueven. Parte de la percepción de Occhialini es que, de media, la estructura molecular se vuelve más doblada cuanto más caliente se pone. Entonces las moléculas se inclinan más y pasan más tiempo con valores mayores de Θ, más cerca de 45 grados. Después de que Occhialini lo pensó durante un tiempo junto con Hancock y los estudiantes de doctorado en física Sahan Handunkanda y Erin Curry, se dieron cuenta de que había una forma geométrica que tenía la misma descripción matemática. Es el péndulo en espiral de Arquímedes.
Cada giro de la espiral está exactamente a la misma distancia del anterior. Ese espaciado, la distancia entre giros, está controlado por Θ. Imagina una línea que se extiende desde el centro de la esfera hasta un punto de la espiral. El ángulo entre esa línea y el polo de la esfera es Θ. ¿Ves la bolita viajando a lo largo de la espiral? Ese es el final de la línea imaginaria. A medida que Θ crece, la bola se mueve hacia el ecuador. Imagine que la bola representa el estado instantáneo del cristal de fluoruro de escandio:los físicos calcularon el promedio estadístico de lo que está haciendo cada molécula del cristal. Notarás que la bola pasa más tiempo cerca del ecuador de la esfera espiral, es decir, tiende a pasar el rato donde Θ es grande. Si la temperatura del cristal desciende y las moléculas se mueven menos, Θ se vuelve más pequeño, cuanto más tiempo pasa la bola cerca del polo de la esfera y menos se encoge el cristal.
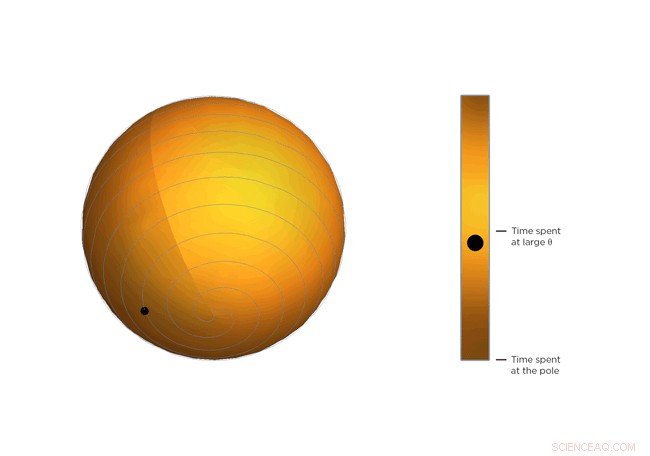
Figura 3. Gire y encoja. La ecuación que describe la rotación de las moléculas de fluoruro de escandio es la misma que la ecuación que describe el movimiento de una bola en un péndulo en espiral de Arquímedes. Observe cómo pasa más tiempo en ángulos más grandes. Crédito:Universidad de Connecticut
Entonces, no solo se puede explicar un fenómeno realmente extraño de un cristal que se encoge a medida que se calienta simplemente asumiendo que las moléculas son rígidas, ¡pero se puede ilustrar con una forma geométrica clásica!
Occhialini era apenas un estudiante de primer año cuando Hancock le presentó el rompecabezas del fluoruro de escandio. Tuvo que aprender matemáticas a medida que avanzaba, pero después de dos semestres de trabajar en ello, había descubierto la ecuación que describía lo que estaba pasando. Ahora en su último año, dice que sus experiencias de investigación en el laboratorio de Hancock han sido parte integral de su experiencia como estudiante.
La ecuación funciona maravillosamente y también explica ciertos aspectos de las mediciones experimentales de rayos X de Hancock.
"Aprendí mucho más investigando de lo que cualquier curso podría haberme dado, "Dice Occhialini.